K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 1
Sửa đề: \(S=2^{100}-2^{99}+2^{98}-...+2^2-2\)
=>\(2\cdot S=2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
=>\(2S+S=2^{100}-2^{99}+2^{98}-...+2^2-2+2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
=>\(3S=2^{101}-2\)
=>\(S=\dfrac{2^{101}-2}{3}\)
13 tháng 11 2023
a: \(A=2^{100}-2^{99}+2^{98}-2^{97}+...+2^2-2\)
=>\(2A=2^{101}-2^{100}+2^{99}-2^{98}+...+2^3-2^2\)
=>\(2A+A=2^{101}-2^{100}+2^{99}-2^{98}+...+2^3-2^2+2^{100}-2^{99}+...+2^2-2\)
=>\(3A=2^{101}-2\)
=>\(A=\dfrac{2^{101}-2}{3}\)
b: Sửa đề: \(A=\dfrac{2\cdot8^4\cdot27^2+4\cdot6^9}{2^7\cdot6^7+2^7\cdot40\cdot9^4}\)
\(A=\dfrac{2\cdot2^{12}\cdot3^6+2^2\cdot2^9\cdot3^9}{2^7\cdot2^7\cdot3^7+2^7\cdot2^3\cdot5\cdot3^8}\)
\(=\dfrac{2^{11}\cdot3^6\left(2^3+3^3\right)}{2^{10}\cdot3^7\left(2^4+5\cdot3\right)}\)
\(=\dfrac{2}{3}\cdot\dfrac{4+27}{16+15}=\dfrac{2}{3}\)
c: \(B=\dfrac{4^5\cdot9^4-2\cdot6^4}{2^{10}\cdot3^8+6^8\cdot20}\)
\(=\dfrac{2^{10}\cdot3^8-2\cdot2^4\cdot3^4}{2^{10}\cdot3^8+2^8\cdot2^2\cdot5\cdot3^8}\)
\(=\dfrac{2^5\cdot3^4\left(2^5\cdot3^4-1\right)}{2^{10}\cdot3^8\left(1+5\right)}=\dfrac{1}{2^5\cdot3^4}\cdot\dfrac{32\cdot81-1}{6}\)
\(=\dfrac{2591}{2^6\cdot3^5}\)
HN
10 tháng 7 2018
297 . 299
= 297 . ( 298 + 1 )
= 297 . 298 + 297
2982 = 298 . 298
= ( 297 + 1 ) . 298
= 297 . 298 + 298
Mà 297 . 298 + 297 < 297 . 298 + 298 nên 297 . 299 < 2982 ( đpcm )
5 tháng 3 2021
Đặt :
\(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+.....+\dfrac{1}{2^{99}}\)
\(\Leftrightarrow2A=3+\dfrac{1}{2}+\dfrac{1}{2^2}+....+\dfrac{1}{2^{98}}\)
\(\Leftrightarrow2A-A=\left(3+\dfrac{1}{2}+....+\dfrac{1}{2^{98}}\right)-\left(1+\dfrac{1}{2}+....+\dfrac{1}{2^{99}}\right)\)
\(\Leftrightarrow A=2-\dfrac{1}{2^{99}}\)
Vậy..
VV
1
19 tháng 9 2016
a) Đặt \(A=5^{300}+5^{299}+...+5\)
\(\Rightarrow A=\left(5^{300}+5^{299}+5^{298}\right)+...+\left(5^3+5^2+5\right)\)
\(\Rightarrow A=5^{298}.\left(5^2+5+1\right)+...+5\left(5^2+5+1\right)\)
\(\Rightarrow A=5^{298}.31+...+5.31\)
\(\Rightarrow A=\left(5^{298}+...+5\right).31⋮31\)
\(\Rightarrow A⋮31\left(đpcm\right)\)
8 tháng 8 2021
*Sửa lại đề*
A = 21+ 22+ 23+ 24 + .. + 2100
A = (21+22) + (23+ 24) +...+ (299+ 2100)
A = 2.(1+2) + 23.(1+2) + .. + 299. (1+2)
A = 2.3 + 23. 3 + .. + 299.3
A = 3 . (21 + 23 + .... + 299)
Mà 3 chia hết cho 3
=> A chia hết cho 3
11 tháng 10 2021
a) \(A=1+2+2^2+2^3+...+2^{99}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{100}\)
\(\Rightarrow A=2A-A=2+2^2+...+2^{100}-1-2-2^2-...-2^{99}=2^{100}-1\)
b) \(A=1+2+2^2+...+2^{99}=\left(1+2+2^2+2^3\right)+2^4\left(1+2+2^2+2^3\right)+...+2^{96}\left(1+2+2^2+2^3\right)\)
\(=15+2^4.15+...+2^{96}.15=15\left(1+2^4+...+2^{96}\right)\)
\(=3.5\left(1+2^4+...2^{96}\right)\) chia hết cho 3 và 5
c) \(A=1+2+2^2+...+2^{99}\)
\(=1+2\left(1+2+2^2\right)+...+2^{97}\left(1+2+2^2\right)\)
\(=1+2.7+...+2^{97}.7=1+7\left(2+...+2^{97}\right)\) chia 7 dư 1
=> A không chia hết cho 7
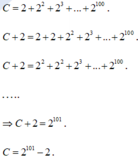
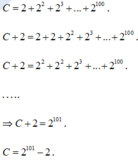
Ta có:
A= 2100-299+298-297+...+22-2
= (2100-299)+(298-297)+...+ (22-2)
= 299+298+297+...+22+2
=> 2A = 2100 + 299+298+297+...+22+2
2A - A = 2100 - 2
A = 2100 - 2
Ta có:
A= 2100-299+298-297+...+22-2
= (2100-299)+(298-297)+...+ (22-2)
= 299+298+297+...+22+2
=> 2A = 2100 + 299+298+297+...+22+2
2A - A = 2100 - 2
A = 2100 - 2