Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi biến cố A: “Chuyến bay của hãng X khởi hành đúng giờ”, biến cố B: “Chuyến bay của hãng Y khởi hành đúng giờ”.
Ta dùng sơ đồ hình cây để mô tả như sau:
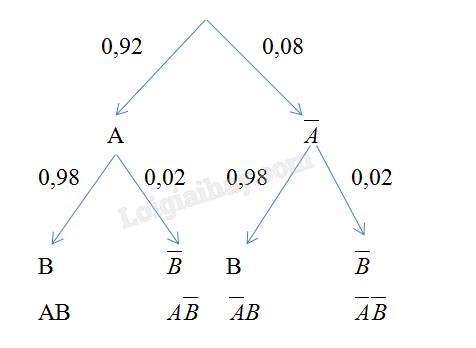
Theo sơ đồ hình cây, ta có:
a) \(P\left( {AB} \right) = 0,92.0,98 = 0,9016\)
b) \(P\left( {A\overline B \cup \overline A B} \right) = 0,92.0,02 + 0,08.0,98 = 0,0968\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,02 = 0,0016\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0016 = 0,9984\)

Ta dùng sơ đồ hình cây để mô tả như sau:
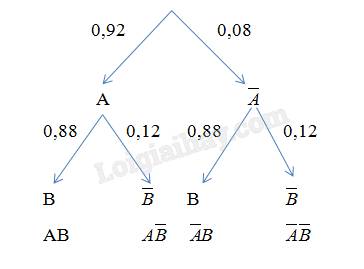
Theo sơ đồ hình cây, ta có:
a) \(P\left( {A\overline B } \right) = 0,92.0,12 = 0,1104\)
b) \(P\left( {\overline A B} \right) = 0,08.0,88 = 0,0704\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,12 = 0,0096\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0096 = 0,9904\)

Chọn C.
Gọi D là biến cố "Cả hai động cơ đều chạy không tốt".Ta thấy A ¯ B ¯ . Hai biến cố A ¯ và B ¯ độc lập với nhau nên P(D=(1-P(A)). (1-P(B))=0,06.

Gọi K là biến cố "Có ít nhất một động cơ chạy tốt",khi đó biến cố đối của K là biến cố D. Do đó
P(K)=1-P(D)=0,94.
Chọn D.

Gọi A là biến cố "Động cơ I chạy tốt", B là biến cố "Động cơ II chạy tốt" C là biến cố "Cả hai động cơ đều chạy tốt".Ta thấy A, B là hai biến cố độc lập với nhau và C=A.B
Ta có P(C)=P(AB)=P(A).P(B)=0,56
Chọn A.

Đáp án B
Mỗi hành khách có 4 cách chọn 1 toa để lên tàu nên số cách 4 hành khách chọn toa để lên tàu là ![]() cách. Suy ra
cách. Suy ra ![]()
Gọi A là biến cố: “một toa có 3 hành khách; một toa có 1 hành khách và hai toa không có hành khách”.
Chon 3 hành khách từ 4 hành khách và xếp 3 hành khách vừa chọn lên 1 trong 4 toa tàu có ![]() cách
cách
Xếp hành khách còn lại lên 1 trong 3 toa tàu còn lại có 3 cách
Suy ra ![]()
Vậy xác suất của biến cố cần tìm là
![]()

Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia”, i=1,2
TH1. Xạ thủ thứ nhất bắn trúng, xạ thủ 2 bắn trượt thì xác suất là:
P A 1 = 1 2 . 1 − 1 3
TH2. Xạ thủ thứ nhất bắn trượt, xạ thủ thứ 2 bắn trúng thì xác suất là:
P A 2 = 1 − 1 2 . 1 3
TH3. Cả 2 xạ thủ đều bắn trượt
P A 3 = 1 − 1 2 . 1 − 1 3
Xác suất của biến cố Y là:
P Y = P A 1 + P A 2 + P A 3 = 5 6
Đáp án. D

a. Xác suất để cả 3 cùng hoạt động tốt:
\(P=0,6.0,7.0,8=0,336\)
b. Xác suất để cả 3 cùng ko hoạt động tốt:
\(P=\left(1-0,6\right)\left(1-0,7\right)\left(1-0,8\right)=0,024\)
c. Xác suất để có đúng 1 động cơ hoạt động tốt:
\(P=0,6.\left(1-0,7\right)\left(1-0,8\right)+\left(1-0,6\right).0,7.\left(1-0,8\right)+\left(1-0,6\right).\left(1-0,7\right).0,8=0,188\)
d. Xác suất có đúng 2 động cơ hoạt động tốt:
\(P=0,6.0,7.\left(1-0,8\right)+0,6.\left(1-0,7\right).0,8+\left(1-0,6\right).0,7.0,8=0,452\)
e. Xác suất để có ít nhất động cơ chạy tốt
\(P=1-0,024=0,976\)
Xác suất để máy bay X khởi hành đúng giờ là:
`1 - 0,92 = 0,08`
Xác suất để máy bay Y khởi hành đúng giờ là:
`1 - 0,98 = 0,02`
Xác suất để duy nhất máy bay X khởi hành đúng giờ là:
`0,08 . 0.98 =` \(\dfrac{49}{625}\)
Xác suất để suy nhất máy bay Y khởi hành đúng giờ là:
`0,02 . 0,92 =` \(\dfrac{23}{1250}\)
Xác suất để chỉ có một trong 2 máy bay khởi hành đúng giờ là:
\(\dfrac{49}{625}+\dfrac{23}{1250}=\dfrac{121}{1250}\)
Đáp số: ...
Xác suất để chuyến bay hoạt động ko đúng giờ lần lượt là 0,08 và 0,02
Có duy nhất 1 trong 2 chuyến đúng giờ khi: X đúng giờ, Y sai giờ hoặc X sai giờ, Y đúng giờ
Xác suất:
\(P=0,92.0,02+0,08.0,98=0,0968\)