Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi biến cố A: “Chuyến bay của hãng X khởi hành đúng giờ”, biến cố B: “Chuyến bay của hãng Y khởi hành đúng giờ”.
Ta dùng sơ đồ hình cây để mô tả như sau:
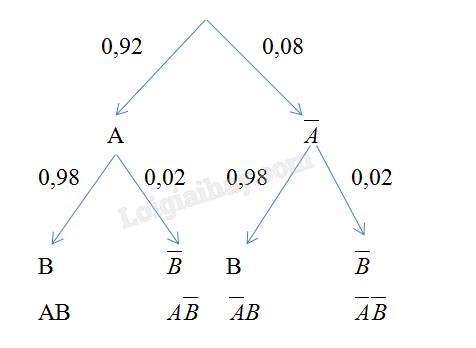
Theo sơ đồ hình cây, ta có:
a) \(P\left( {AB} \right) = 0,92.0,98 = 0,9016\)
b) \(P\left( {A\overline B \cup \overline A B} \right) = 0,92.0,02 + 0,08.0,98 = 0,0968\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,02 = 0,0016\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0016 = 0,9984\)

Chọn C.
Gọi D là biến cố "Cả hai động cơ đều chạy không tốt".Ta thấy A ¯ B ¯ . Hai biến cố A ¯ và B ¯ độc lập với nhau nên P(D=(1-P(A)). (1-P(B))=0,06.

Gọi K là biến cố "Có ít nhất một động cơ chạy tốt",khi đó biến cố đối của K là biến cố D. Do đó
P(K)=1-P(D)=0,94.
Chọn D.

Gọi A là biến cố "Động cơ I chạy tốt", B là biến cố "Động cơ II chạy tốt" C là biến cố "Cả hai động cơ đều chạy tốt".Ta thấy A, B là hai biến cố độc lập với nhau và C=A.B
Ta có P(C)=P(AB)=P(A).P(B)=0,56
Chọn A.

Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
![]()
Chọn A

Gọi xác suất bộ phận 1 bị hỏng là x với \(0\le x\le1\)
Xác suất không bị hỏng của 2 bộ phận lần lượt là \(1-x\) và \(0,2\)
Xác suất có đúng 1 bộ phận bị hỏng (gồm 2 TH1: 1 hỏng 2 bình thường, 1 bình thường 2 hỏng):
\(x.0,2+\left(1-x\right).0,8=0,38\)
\(\Rightarrow x=0,7\)

Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
c) Gọi X là biến cố :” có ít nhất một động cơ chạy tốt” thì X là biến cố đối của :
![]()
Chọn D