PD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
L
1 tháng 2 2016
a, Ta thấy với a,b >0 thì \(\frac{a}{b}<\frac{a+n}{b+n}\), với a,b<0 thì \(\frac{a}{b}>\frac{a+\left(-n\right)}{b+\left(-n\right)}\) \(\left(n\in Z;\right)n>0\)
Vậy ta sắp xếp như sau:
\(-\frac{8}{9};-\frac{6}{7};-\frac{4}{5};-\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{5}{6};\frac{7}{8};\frac{9}{10}\)
L
1 tháng 2 2016
b, Có:
\(\frac{0}{23}=0\)
\(-\frac{14}{5}<-1<\frac{-15}{19}<-\frac{15+\left(-2\right)}{19+\left(-2\right)}=-\frac{13}{17}\)
\(\frac{5}{2}>\frac{4}{2}=2>\frac{11}{7}=\frac{99}{63}>\frac{13}{9}=\frac{91}{63}\)
Vậy ta sắp xếp như sau:
\(-\frac{14}{5};-\frac{15}{19};-\frac{13}{17};0;\frac{13}{9};\frac{11}{7};\frac{5}{2}\)
NL
1
SY
28 tháng 3 2016
\(\frac{\frac{1}{4}+\frac{1}{24}+\frac{1}{124}}{\frac{3}{4}+\frac{3}{24}+\frac{3}{124}}\) + \(\frac{\frac{2}{7}+\frac{2}{17}+\frac{2}{127}}{\frac{3}{7}+\frac{3}{17}+\frac{3}{127}}\)
= \(\frac{\frac{1}{4}+\frac{1}{24}+\frac{1}{124}}{3.\left(\frac{1}{4}+\frac{1}{24}+\frac{1}{124}\right)}\) + \(\frac{2.\left(\frac{1}{7}+\frac{1}{17}+\frac{1}{127}\right)}{3.\left(\frac{1}{7}+\frac{1}{17}+\frac{1}{127}\right)}\)
= \(\frac{1}{3}\) + \(\frac{2}{3}\) = 1
3 tháng 4 2016
a) \(\frac{7}{11}-\left(\frac{3}{5}+\frac{7}{11}\right)=-\frac{3}{5}\)
b) \(\left(\frac{11}{22}+\frac{5}{11}\right)-\frac{19}{22}=\frac{1}{11}\)
c) \(\frac{2}{9}.\frac{4}{5}+\frac{2}{9}.\frac{14}{5}=\frac{4}{5}\)
d) \(-\frac{3}{2}.\frac{7}{10}-\frac{3}{2}.\frac{1}{10}=-\frac{6}{5}\)
e) \(\left(0,75-1+\frac{1}{4}\right):\left(\frac{1515}{1616}+\frac{1616}{1717}\right)=0\)
DT
2
HX
3
NH
3 tháng 2 2016
Đáp án A. Theo quy luật : cứ sau vòng lặp 2 số (vd 7-8) thì số thứ nhất giảm đi 1 đơn vị (vd 7->6) và số thứ 2 tăng lên 1 đơn vị (vd 8->9)
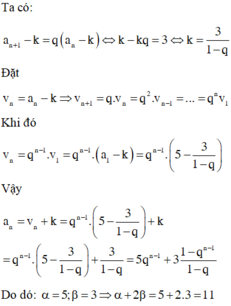
bạn hỏi thầy cô là dc
bạn sheach lên mạng cũng dc