Tính rồi tìm nghịch đảo: P = 1 − 1 2 1 − 1 3...

Khách

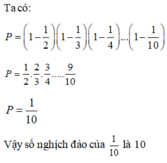
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

28 tháng 3 2019

Tính rồi tìm nghịch đảo: P = 1 − 1 2 1 − 1 3 1 − 1 4 ... 1 − 1 10

#Toán lớp 6

Cao Minh Tâm

28 tháng 3 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Danh Thảo Quyên

27 tháng 3 2017 - olm

tính tích sau rồi tìm số nghịch đảo của kết quả:

T= (1- 1/3) . (1- 1/5). (1- 1/7) . ( 1- 1/9) . (1- 1/11). (1-1/2). (1-1/4). (1-1/6) . ( 1-1/8). (1-1/10)

#Toán lớp 6

ngo vinh thien

27 tháng 3 2017

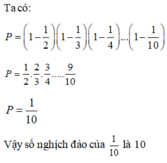
T=(1-1/2).(1-1/3).(1-1/4)....(1-1/10)

T=1/2.2/3.3/4.4/5....9/10

T=1.9/10

T=9/10

BÀI TOÁN DỄ NHẤT ĐẤY

Đúng(0)

Lê Anh Thư

19 tháng 8 2016

2.Tính tích sau rồi tìm số nghịch đảo của kết quả:

T=( 1-1/3) (1-1/5) (1-1/7) ( 1- 1/9) (1-1/11) (1-1/2) ( 1-1/4) ( 1-1/6) (1-1/8) (1-1/10).

Mk tick nha!!!!!!!!!!!!!!!!!

#Toán lớp 6

Lightning Farron

19 tháng 8 2016

T=( 1-1/3) (1-1/5) (1-1/7) ( 1- 1/9) (1-1/11) (1-1/2) ( 1-1/4) ( 1-1/6) (1-1/8) (1-1/10)

\(=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right)...\left(1-\frac{1}{11}\right)\)

\(=\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot...\cdot\frac{10}{11}\)

\(=\frac{1\cdot2\cdot3\cdot...\cdot10}{2\cdot3\cdot4\cdot...\cdot11}\)

\(=\frac{1}{11}\)

Đúng(0)

Isolde Moria

19 tháng 8 2016

Ta có

\(A=\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right).....\left(1-\frac{1}{11}\right)\left(1-\frac{1}{2}\right)\left(1-\frac{1}{4}\right)......\left(1-\frac{1}{10}\right)\)

\(\Leftrightarrow A=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right).....\left(1-\frac{1}{11}\right)\)

\(\Leftrightarrow A=\frac{1.2.3.....10}{2.3.4.....11}=\frac{1}{11}\)

Đúng(1)

cún bông

25 tháng 3 2018 - olm

1:tìm giá trih của a, b, c, d rồi tìm số nghịch đảo của chúng;

a= 1/2 - 1/3

b= 1/10 x 2/3 +1

c= 2/5- 1/21

d= -6 - (2.1/3)

2: timd các cặp số nghịch đảo của nhau trong các cặp số sau:

a) 0,2 và 5

b) 0,4 và 4

c) 1/3 và 3,1

d) 8/3 và 0,375

#Toán lớp 6

Nguyễn Lan Phương

16 tháng 7 2015 - olm

Cho C = 0,5 + 1/3 + 0,4 +5/7 +1/6 - 4/35 + 1/41

D = 1/90- 1/72- 1/56 - 1/42- 1/30 - 1/12 - 1/6 -1/2

Tính C và D rồi tìm tích các số nghịch đảo của C và D

#Toán lớp 6

Moon

31 tháng 3 2021

tìm tích rồi tìm số nghịch đảo của chúngT=(1- \(\dfrac{1}{3}\) )(1- \(\dfrac{1}{5}\))(1-\(\dfrac{1}{7}\) )(1- \(\dfrac{1}{9}\) )(1- \(\dfrac{1}{11}\) )(1- \(\dfrac{1}{2}\))(1- \(\dfrac{1}{4}\))(1- \(\dfrac{1}{6}\))(1- \(\dfrac{1}{8}\))(1- \(\dfrac{1}{10}\)...

Đọc tiếp

#Toán lớp 6

Nguyễn Lê Phước Thịnh

31 tháng 3 2021

Ta có: \(P=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{11}\right)\)

\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\cdot\dfrac{-10}{11}\)

\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{9}{10}\cdot\dfrac{10}{11}\)

\(=\dfrac{1}{11}\)

Đúng(1)

Phan Gia Nhi

21 tháng 3 2017 - olm

Tính giá trị của a,b,c,d rồi tìm số nghịch đảo của chúng

a = 1/3 - 1/4

b = 2/7 . 14/5 -1

c = 3/4 - 1/25 . 5

d = -8 . (6 . 1/24)

Các bạn tính chi tiết từng phép tính giúp mình nhé

Mình cảm ơn các bạn

#Toán lớp 6

Sách Giáo Khoa

15 tháng 5 2017

Tìm tích sau rồi tìm số nghịch đảo của kết quả :

\(T=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{11}\right)\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{8}\right)\left(1-\dfrac{1}{10}\right)\)

#Toán lớp 6

Hàn Thất Lục

15 tháng 5 2017

\(T=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{8}\right)\left(1-\dfrac{1}{10}\right)\)\(\Rightarrow T=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}.\dfrac{8}{9}.\dfrac{10}{11}.\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.\dfrac{7}{8}.\dfrac{9}{10}\)

\(\Rightarrow=\dfrac{1}{11}\)

\(\Rightarrow\) Số nghịch đảo của T là \(11\)

Đúng(0)