Question

[vô danh]

tính nhanh 

\(B=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\)

Answer 1

[Nguyễn Thị Thương Hoài]

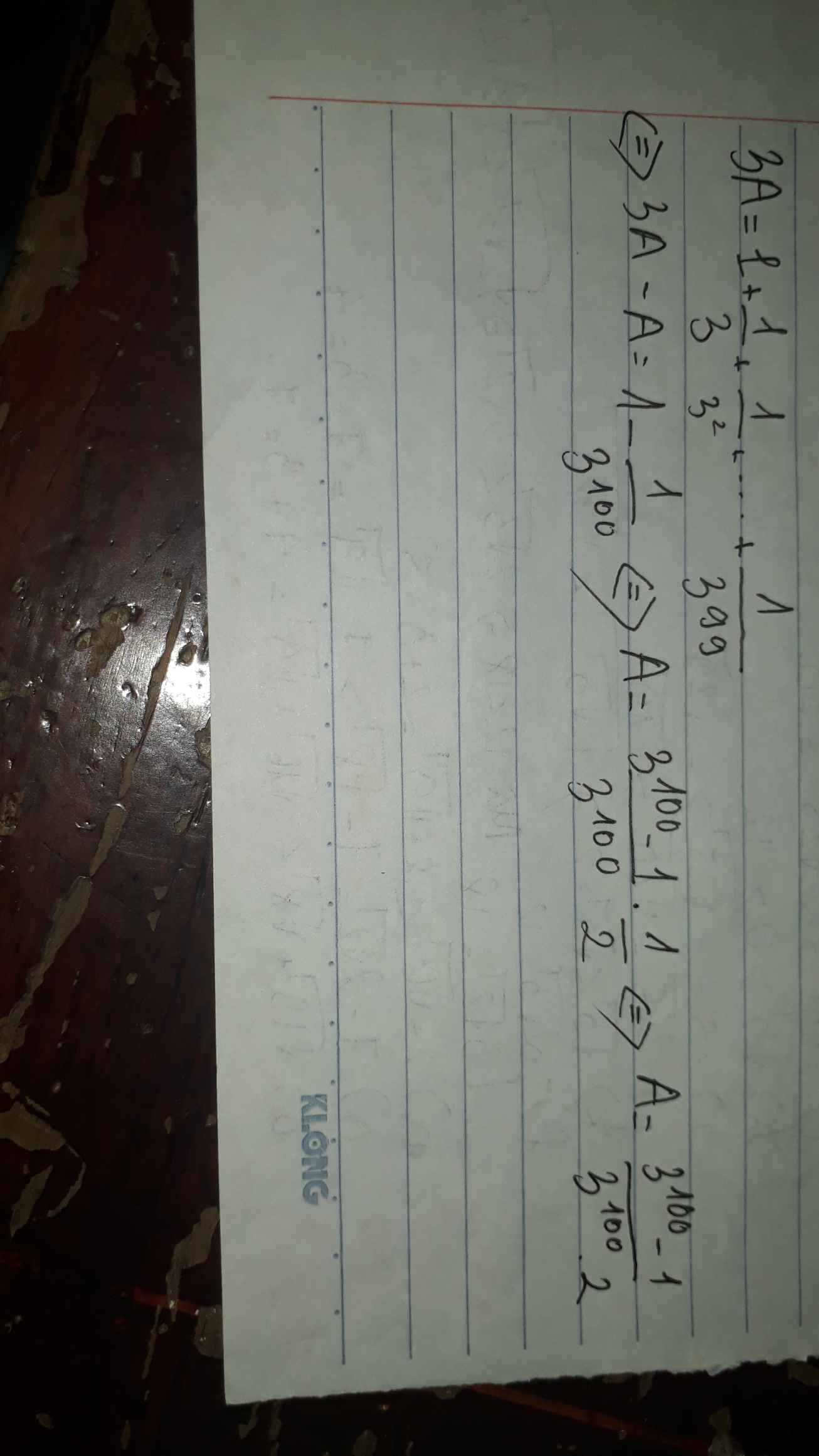
   D = \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+...+ \(\dfrac{1}{3^{100}}\)

3.D = 1  + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) +...+ \(\dfrac{1}{3^{99}}\)

3D - D = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\)+...+ \(\dfrac{1}{3^{99}}\) - (\(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+...+\(\dfrac{1}{3^{100}}\))

2D       = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + ... + \(\dfrac{1}{3^{99}}\) - \(\dfrac{1}{3}\) - \(\dfrac{1}{3^2}\) - \(\dfrac{1}{3^3}\)-...-\(\dfrac{1}{3^{100}}\)

2D      = (\(\dfrac{1}{3}\) - \(\dfrac{1}{3}\)) + (\(\dfrac{1}{3^2}\) - \(\dfrac{1}{3^2}\)) + (\(\dfrac{1}{3^3}\)-\(\dfrac{1}{3^3}\))+...+(\(\dfrac{1}{3^{99}}\)-\(\dfrac{1}{3^{99}}\)) + (1 - \(\dfrac{1}{3^{100}}\))

2D      = 0 + 0 + 0 +...+0 + 1 - \(\dfrac{1}{3^{100}}\) 

2D     = 1 - \(\dfrac{1}{3^{100}}\)

2D    = \(\dfrac{3^{100}-1}{3^{100}.2}\)

Answer 2

[Citii?]

\(B=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\)

\(\Rightarrow3B=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)

\(\Rightarrow3B-B=\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\)

\(\Rightarrow2B=1-\dfrac{1}{3^{100}}\)

\(\Rightarrow B=\dfrac{1-\dfrac{1}{3^{100}}}{2}\)