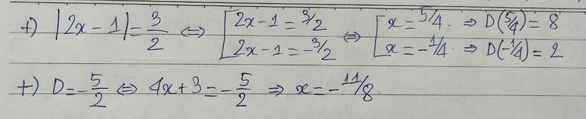Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|2x-1\right|=\dfrac{3}{2}\\ \Rightarrow\left[{}\begin{matrix}2x-1=\dfrac{3}{2}\\2x-1=-\dfrac{3}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
Thay \(x=\dfrac{5}{4}\) vào D ta có:
\(D=4x+3=4.\dfrac{5}{4}+3=5+3=8\)
Thay \(x=-\dfrac{1}{4}\) vào D ta có:
\(D=4.\dfrac{-1}{4}+3=-1+3=2\)
Để \(D=\dfrac{3}{2}\)
\(\Leftrightarrow4x+3=\dfrac{3}{2}\\ \Leftrightarrow4x=-\dfrac{3}{2}\\ \Leftrightarrow x=-\dfrac{3}{8}\)

khi |x-2|=1 => hoặc là x-2=1 =>x=3
hoặc là x-2=-1 =>x=1
sau đó bạn thay từng giá trị của x vào biểu thức rồi tính là ra thôi. ủng hộ mik nha

cho đa thứcF(x)xác định với mọi x thỏa mãn điều kiện f(x)+3*f(1/2)=x2. tính f(2)
cho đa thứcF(x)xác định với mọi x, biết: f(x)+x*f(-x)=x+1. tính(1)
Toán lớp 7
ai tích mình mình tích lại nh nha


2x−3y/5=5y−2z/3=3z−5x/2=10x-15y/25=15y-6z/9=6z-10x/4=...+..+..../25+9+4=0/31=0
=> 2x=3y; 5y=2z ; 3z=5x => x/3=y/2; y/2=z/5
=> x/3=y/2 =z/5 = 12x/36=5y/10=3z/15= (12x+5y-3z)/31
x/3 = 3y/6=2z/10 = (x-3y+2z)/7
=> (12x+5y-3z)/ (x-3y+2z)=31/7

Xin lỗi bn nhiều nha TH1 mk lm sai :
\(x-2=1\Leftrightarrow x=3\)
Thay x = 3 vào biểu thức A ta có :
\(A=6.3^2+5.3-2=6.9+5.3-2=54+15-2=67\)
Vậy giá trị của biểu thức A tại x = 3 là 67
Ta có : \(|x-2|=1\Leftrightarrow\orbr{\begin{cases}x-2=1\\x-2=-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=1\end{cases}}\)
Đặt \(A=6x^2+5x-2\)
Thay x = -1 vào biểu thức A ta có :
\(A=6.\left(-1\right)^2+5.\left(-1\right)-2=6.1+\left(-5\right)-2=6-5-2=-1\)
Vậy giá trị của biểu thức A tại x = -1 là -1
Thay x = 1 vào biểu thức A ta có :
\(A=6.1^2+5.1-2=6.1+5-2=6+5-2=9\)
Vậy giá trị của biểu thức A tại x = 1 là 9

Bài 1:
b) ĐKXĐ: \(x\ne3\)
Ta có: \(\dfrac{3-x}{20}=\dfrac{-5}{x-3}\)
\(\Leftrightarrow\dfrac{x-3}{-20}=\dfrac{-5}{x-3}\)
\(\Leftrightarrow\left(x-3\right)^2=100\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=10\\x-3=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=13\left(nhận\right)\\x=-7\left(nhận\right)\end{matrix}\right.\)
Vậy: \(x\in\left\{13;-7\right\}\)