Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\frac{11.3^{29}-3^{30}}{2^2.3^{28}}=\frac{3^{29}\left(11-3\right)}{2^2.3^{28}}=\frac{3^{29}.2^3}{2^2.3^{28}}=3.2=6.\)
\(\frac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}=\frac{11.3^{22}.3^7-\left(3^2\right)^{15}}{2^2.\left(3^{14}\right)^2}=\frac{11.3^{29}-3^{30}}{2^2.3^{28}}\)
\(=\frac{3^{29}\left(11-3\right)}{2^2.3^{28}}=\frac{3.8}{4}=\frac{24}{4}=6\)
Đáp số: \(6\)

\(\dfrac{11\cdot3^7\cdot9^7-9^{15}}{\left(2\cdot3^{14}\right)^2}\)
\(=\dfrac{11\cdot3^7\cdot3^{14}-3^{30}}{2^2\cdot3^{28}}\)
\(=\dfrac{3^{21}\left(11-3^9\right)}{2^2\cdot3^{28}}\)
\(=\dfrac{11-3^9}{2^2\cdot3^7}\)

\(a)245^2+490\cdot54+54^2-199^2\\=(245^2+2\cdot245\cdot54+54^2)-199^2\\=(245+54)^2-199^2\\=299^2-199^2\\=(299-199)(299+199)\\=100\cdot498\\=49800\\---\\b)356^2-356\cdot246+123^2-133^2\\=(356^2-2\cdot356\cdot123+123^2)-133^2\\=(356-123)^2-133^2\\=233^2-133^2\\=(233-133)(233+133)\\=100\cdot366\\=36600\)
\(---\)
\(c)468^2-412^2-110\cdot412-55^2\\=468^2-(412^2+110\cdot412+55^2)\\=468^2-(412^2+2\cdot412\cdot55+55^2)\\=468^2-(412+55)^2\\=468^2-467^2\\=(468-467)(468+467)\\=1\cdot935\\=935\\---\)
\(d)615^2+250\cdot615+125^2-540^2\\=(615^2+2\cdot615\cdot125+125^2)-540^2\\=(615+125)^2-540^2\\=740^2-540^2\\=(740-540)(740+540)\\=200\cdot1280\\=256000\)
#\(Toru\)


A=11.322.37-915/(2.314)2
A=11.329-915/22.328
A=11.329-(32)15/4.328
A=11.329-330/4.328
A=11.329-329.3/4.328
A=329.(11-3)/328.4
A=329.8/328.4
A=3.8/4
A=24/4
A=6

Siêu tốc tổng quát: \(\frac{1}{n.\left(n+1\right)}=\frac{1}{n}-\frac{1}{n+1}\)áp vào
\(A=\frac{1}{1}-\frac{1}{14}=1-\frac{1}{14}\)
A=(2-1)/1.2+(3-2)/2.3+...+(14-13)/13.14
A=1-1/2+1/2-1/3+...+1/13-1/14
A=1-1/14=13/14

\(A=\left|x-13\right|+\left|x-14\right|+\left|x-15\right|+\left|x-16\right|+\left|x-17\right|-10\)
\(=\left(\left|x-13\right|+\left|x-16\right|\right)+\left(\left|x-14\right|+\left|x-17\right|\right)-10+\left|x-15\right|\)
\(=\left(\left|x-13\right|+\left|16-x\right|\right)+\left(\left|x-14\right|+\left|17-x\right|\right)-10+\left|x-15\right|\)
\(\Rightarrow A\ge\left|x-13+16-x\right|+\left|x-14+17-x\right|-10+\left|x-15\right|\)
\(=\left|3\right|+\left|3\right|-10+\left|x-15\right|\)\(=3+3-10+\left|x-15\right|=-6+\left|x-15\right|\)
Vì \(\left|x-15\right|\ge0\forall x\)\(\Rightarrow A\ge-6\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x-13\right)\left(16-x\right)\ge0\\\left(x-14\right)\left(17-x\right)\ge0\\x-15=0\end{cases}}\Leftrightarrow\hept{\begin{cases}13\le x\le16\\14\le x\le17\\x=15\end{cases}}\Leftrightarrow x=15\)
Vậy \(minA=-6\Leftrightarrow x=15\)

\(=\dfrac{11\cdot3^{21}-3^{30}}{2^2\cdot3^{28}}=\dfrac{3^{21}\left(11-3^7\right)}{2^2\cdot3^{28}}=\dfrac{-2176}{2^2\cdot3^7}=\dfrac{-2176}{8748}=\dfrac{-544}{2187}\)

ta có: x = 2018 => 2019 = x + 1. Do đó:
\(C=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-\left(x+1\right)x^{12}+...+\left(x+1\right)x-1.\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-x^{13}-x^{12}+...+x^2+x-1.\)
\(=x-1=2019-1=2018\)
Vậy C = 2018 với x = 2018.
Học tốt nhé ^3^
\(Ta \) \(có :\)
\(x = 2018\)\(\Leftrightarrow\)\(x + 1 = 2019\)
\(Thay \) \(x + 1 = 2019\)\(vào \) \(C , ta \) \(được :\)
\(C = x\)\(15\)\(- ( x + 1 ).x\)\(14\)\(+ ( x + 1 ).x\)\(13\) \(- ( x + 1 ).x\)\(12\) \(+ ...+ ( x + 1 ).x - 1\)
\(C = x\)\(15\)\(- x\)\(15\)\(- x\)\(14\) \(+ x\)\(14\) \(+ x\)\(13\)\(- x\)\(13\)\(- x\)\(12\)\(+ ... + x^2 + x - 1\)
\(C = x - 1\)
\(Thay \) \(x = 2018\) \(vào \) \(C\) \(, ta \) \(được :\)
\(C = 2018 - 1 = 2017\)
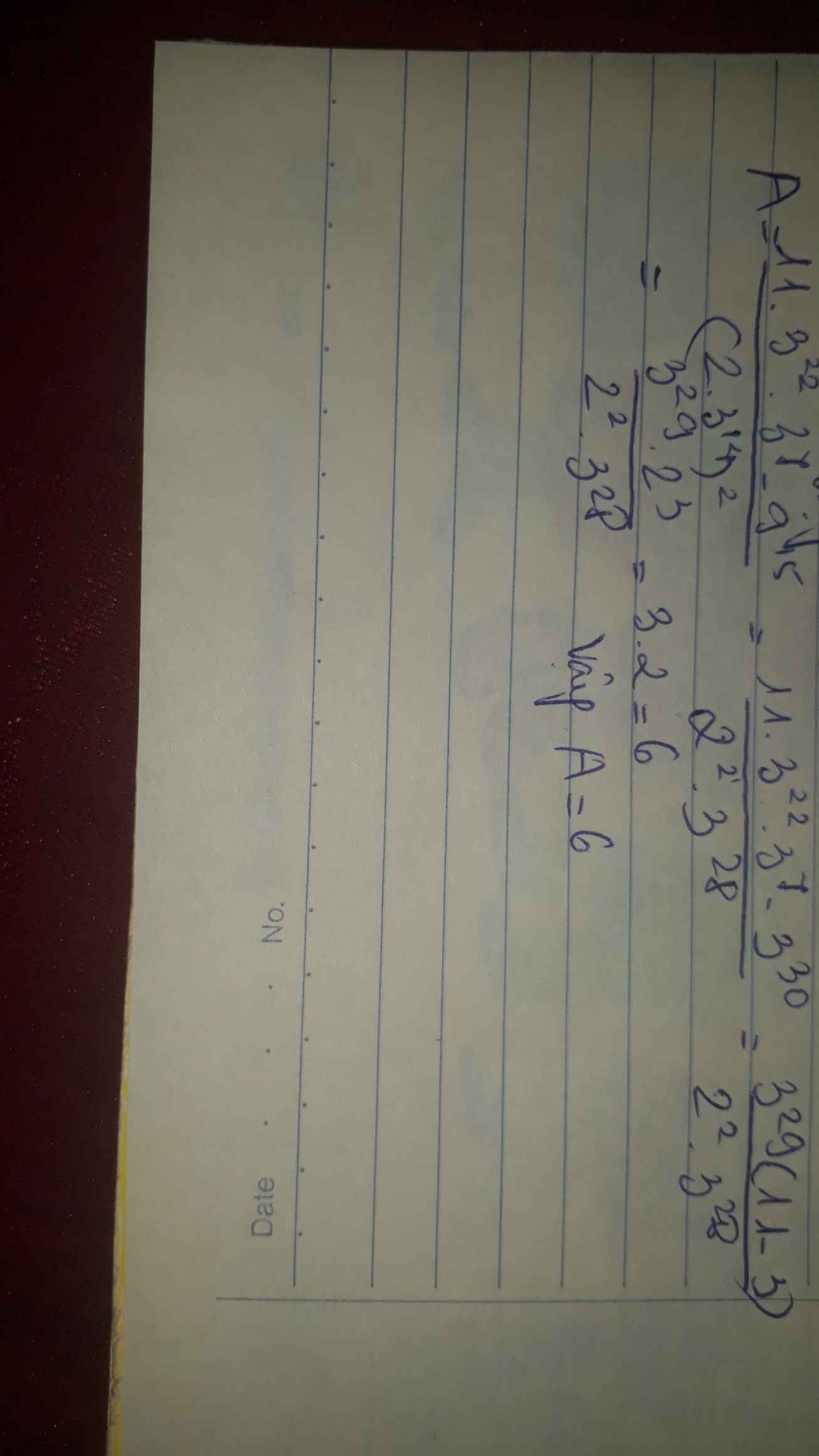
* là gì đó bạn
@Hưng Què Dấu nhân nhé