Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(D=\dfrac{4}{8\cdot13}+\dfrac{4}{13\cdot18}+\dfrac{4}{18\cdot23}+...+\dfrac{4}{253\cdot258}\\ =\dfrac{4}{5}\cdot\dfrac{5}{8\cdot13}+\dfrac{4}{5}\cdot\dfrac{5}{13\cdot18}+\dfrac{4}{5}\cdot\dfrac{5}{18\cdot23}+...+\dfrac{4}{5}\cdot\dfrac{5}{253\cdot258}\\ =\dfrac{4}{5}\left(\dfrac{5}{8\cdot13}+\dfrac{5}{13\cdot18}+\dfrac{5}{18\cdot23}+...+\dfrac{5}{253\cdot258}\right)\\ =\dfrac{4}{5}\cdot\left(\dfrac{1}{8}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{23}+...+\dfrac{1}{253}-\dfrac{1}{258}\right)\\ =\dfrac{4}{5}\cdot\left(\dfrac{1}{8}-\dfrac{1}{258}\right)\\ =\dfrac{4}{5}\cdot\dfrac{125}{1032}\\ =\dfrac{25}{258}\)
ta có
Tính:
\(\dfrac{4}{8.13}+\dfrac{4}{13.18}+....+\dfrac{4}{253.258}\)
= 4 (\(\dfrac{1}{8.13}+\dfrac{1}{13.18}+.....+\dfrac{1}{253.258}\))
=\(\dfrac{4}{5}\left(\dfrac{1}{8}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{18}+...+\dfrac{1}{253}-\dfrac{1}{258}\right)\)
=\(\dfrac{4}{5}\left(\dfrac{1}{8}-\dfrac{1}{258}\right)\)
=\(\dfrac{25}{258}\)

\(\frac{4}{8.13}+\frac{4}{13.18}+\frac{4}{18.24}+...+\frac{4}{253.258}\)
\(=\frac{4}{5}\cdot\left(\frac{1}{8}-\frac{1}{13}+\frac{1}{13}-\frac{1}{18}+\frac{1}{18}-\frac{1}{23}+...+\frac{1}{253}-\frac{1}{258}\right)\)
\(=\frac{4}{5}\cdot\left(\frac{1}{8}-\frac{1}{258}\right)\)
\(=\frac{4}{5}\cdot\frac{125}{1032}\)
\(=\frac{25}{258}\)
\(\frac{4}{8.13}+\frac{4}{13.18}+\frac{4}{18.23}+...+\frac{4}{253.258}\)
\(=\frac{4}{5}\left(\frac{5}{8.13}+\frac{5}{13.18}+\frac{5}{18.23}+...+\frac{5}{253.258}\right)\)
\(=\frac{4}{5}\left(\frac{1}{8}-\frac{1}{13}+\frac{1}{13}-\frac{1}{18}+\frac{1}{18}-\frac{1}{23}+...+\frac{1}{253}-\frac{1}{258}\right)\)
\(=\frac{4}{5}\left(\frac{1}{8}-\frac{1}{258}\right)\)
\(=\frac{4}{5}.\frac{125}{1032}=\frac{25}{258}\)

2A=1-1/2+1/2^2-...+1/2^98-1/2^99
=>3A=1-1/2^100
=>\(A=\dfrac{2^{100}-1}{3\cdot2^{100}}\)

\(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2021.2022}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
\(B=\dfrac{4}{3.7}+\dfrac{4}{7.11}+\dfrac{4}{11.15}+...+\dfrac{4}{107.111}\)
\(=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{107}-\dfrac{1}{111}\)
\(=\dfrac{1}{3}-\dfrac{1}{111}=\dfrac{12}{37}\)

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

\(B=\frac{1}{3}.b+\frac{2}{9}.b– b: \frac{9}{4}= \frac{1}{3}.b+\frac{2}{9}.b – b. \frac{4}{9}\)
\(=b(\frac{1}{3}+\frac{2}{9}-\frac{4}{9})=b. (\frac{3}{9}+\frac{2}{9}-\frac{4}{9})= b. \frac{1}{9} \)
Thay \(b=\frac{9}{10}\) vào B, ta được
B= \(b=\frac{9}{10}. \frac{1}{9}= \frac{1}{10}\)

\(A=\frac{1}{7\cdot12}+\frac{1}{12\cdot17}+\frac{1}{17\cdot22}+...+\frac{1}{52\cdot57}\)
\(A=\frac{1}{5}\left(\frac{5}{7\cdot12}+\frac{5}{12\cdot17}+\frac{5}{17\cdot22}+...+\frac{5}{52\cdot57}\right)\)
\(A=\frac{1}{5}\left(\frac{1}{7}-\frac{1}{12}+\frac{1}{12}-\frac{1}{17}+...+\frac{1}{52}-\frac{1}{57}\right)\)
\(A=\frac{1}{5}\left(\frac{1}{7}-\frac{1}{57}\right)=\frac{1}{5}\cdot\frac{50}{399}=\frac{10}{399}\)
\(B=\frac{10}{8\cdot13}+\frac{10}{13\cdot18}+\frac{10}{18\cdot23}+...+\frac{10}{253\cdot258}\)
\(B=\frac{10}{5}\left(\frac{5}{8\cdot13}+\frac{5}{13\cdot18}+\frac{5}{18\cdot23}+...+\frac{5}{253\cdot258}\right)\)
\(B=2\left(\frac{1}{8}-\frac{1}{13}+\frac{1}{13}-\frac{1}{18}+...+\frac{1}{253}-\frac{1}{258}\right)\)
\(B=2\left(\frac{1}{8}-\frac{1}{258}\right)=2\cdot\frac{125}{1032}=\frac{125}{516}\)
*Cái đây giải thích hơi bị " khó hiểu " :
Chỗ mẫu (12 - 7) = (17 - 12) = ... = (57 - 52) = 5
Tử là 1 , mẫu là 5 nên tử/mẫu = 1/5
Hay \(\frac{1}{5}\left(\frac{5}{7\cdot12}+\frac{5}{12\cdot17}+...+\frac{5}{52\cdot57}\right)\)
Còn bạn Trương Bùi Linh thì :
Mẫu = (13 - 8) = (18 - 13) = (23 - 18) = ... = 5
Tử là 10,mẫu là 5 => tử / mẫu = 10/5 = 2

a) Ta có: \(\left|2x-\dfrac{1}{3}\right|\ge0\forall x\)
\(\Leftrightarrow\left|2x-\dfrac{1}{3}\right|-\dfrac{7}{4}\ge-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi \(2x=\dfrac{1}{3}\)
hay \(x=\dfrac{1}{6}\)
Vậy: \(A_{min}=-\dfrac{7}{4}\) khi \(x=\dfrac{1}{6}\)
b) Ta có: \(\dfrac{1}{3}\left|x-2\right|\ge0\forall x\)
\(\left|3-\dfrac{1}{2}y\right|\ge0\forall y\)
Do đó: \(\dfrac{1}{3}\left|x-2\right|+\left|3-\dfrac{1}{2}y\right|\ge0\forall x,y\)
\(\Leftrightarrow\dfrac{1}{3}\left|x-2\right|+\left|3-\dfrac{1}{2}y\right|+4\ge4\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\3-\dfrac{1}{2}y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=6\end{matrix}\right.\)
Vậy: \(B_{min}=4\) khi x=2 và y=6

\(=4\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\right)=4\cdot\dfrac{2014}{2015}=\dfrac{8056}{2015}\)
\(\dfrac{4}{1.2}+\dfrac{4}{2.3}+...+\dfrac{4}{2014.2015}\\ =4\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2014.2015}\right)\\ =4\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\right)\\ =4\left(1-\dfrac{1}{2015}\right)\\ =4.\dfrac{2014}{2015}\\ =\dfrac{8056}{2015}\)
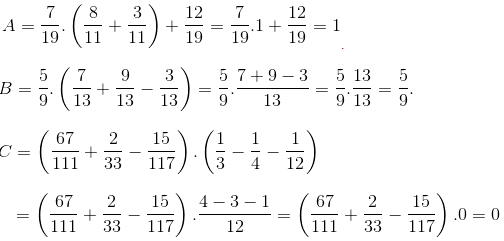
\(\dfrac{5b}{4}=\dfrac{5}{8.13}+\dfrac{5}{13.18}+\dfrac{5}{18.23}+...+\dfrac{5}{253.258}\\ =\dfrac{1}{8}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{23}+...+\dfrac{1}{253}-\dfrac{1}{258}\\ =\dfrac{1}{8}-\dfrac{1}{258}=\dfrac{125}{1032}\\ =>b=\dfrac{25}{258}\)
\(B=\dfrac{4}{8\cdot13}+\dfrac{4}{13\cdot18}+\dfrac{4}{18\cdot23}+...+\dfrac{1}{253\cdot258}\)
\(B=4\left(\dfrac{1}{8\cdot13}+\dfrac{1}{13\cdot18}+\dfrac{1}{18\cdot23}+...+\dfrac{1}{253\cdot258}\right)\)
\(B=\dfrac{4}{5}\left(\dfrac{5}{8\cdot13}+\dfrac{5}{13\cdot18}+\dfrac{5}{18\cdot23}+...+\dfrac{5}{253\cdot258}\right)\)
\(B=\dfrac{4}{5}\left(\dfrac{1}{8}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{23}+...+\dfrac{1}{253}-\dfrac{1}{258}\right)\)
\(B=\dfrac{4}{5}\left(\dfrac{1}{8}-\dfrac{1}{258}\right)\)
\(B=\dfrac{4}{5}\cdot\dfrac{125}{1032}=\dfrac{25}{258}\)