Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P.sin\left(\dfrac{\pi}{7}\right)=sin\dfrac{\pi}{7}.cos\dfrac{\pi}{7}.cos\dfrac{2\pi}{7}.cos\dfrac{4\pi}{7}\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=\dfrac{1}{2}sin\dfrac{2\pi}{7}cos\dfrac{2\pi}{7}cos\dfrac{4\pi}{7}\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=\dfrac{1}{4}sin\dfrac{4\pi}{7}cos\dfrac{4\pi}{7}\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=\dfrac{1}{8}sin\dfrac{8\pi}{7}=\dfrac{1}{8}sin\left(\pi+\dfrac{\pi}{7}\right)\)
\(\Leftrightarrow P.sin\dfrac{\pi}{7}=-\dfrac{1}{8}sin\dfrac{\pi}{7}\)
\(\Rightarrow P=-\dfrac{1}{8}\)

Chọn B.
Ta có: B = ( cos00 + cos1800) + (cos200 + cos1600) +...+ cos800 + cos1000)
= (cos00 - cos00) + (cos200 - cos 200) + ... + (cos800 - cos800) = 0

\(A.sin\dfrac{\pi}{7}=sin\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=\dfrac{1}{2}sin\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=\dfrac{1}{4}sin\left(\dfrac{4\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=\dfrac{1}{8}sin\left(\dfrac{8\pi}{7}\right)\)
\(=\dfrac{1}{8}sin\left(\pi+\dfrac{\pi}{7}\right)=\dfrac{1}{8}sin\left(-\dfrac{\pi}{7}\right)\)
\(=-\dfrac{1}{8}sin\left(\dfrac{\pi}{7}\right)\)
\(\Rightarrow A=-\dfrac{1}{8}\)

\(E=\)\(cos^273+1-sin^247+cos73\left(cos120.cos73+sin120.sin73\right)\)
\(=cos^273+1-\left(sin120.cos73-cos120.sin73\right)^2-\dfrac{1}{2}.cos^273+\dfrac{\sqrt{3}}{2}cos73.sin73\)
\(=cos^273+1-\left(\dfrac{\sqrt{3}}{2}.cos73+\dfrac{1}{2}.sin73\right)^2-\dfrac{1}{2}.cos73^2+\dfrac{\sqrt{3}}{2}cos73.sin73\)
\(=\dfrac{1}{2}cos^273+1-\left(\dfrac{3}{4}cos^273+\dfrac{\sqrt{3}}{2}.cos73.sin73+\dfrac{1}{4}sin^273\right)+\dfrac{\sqrt{3}}{2}.cos73.sin73\)
\(=1-\dfrac{1}{4}.cos^273-\dfrac{1}{4}.sin^273\)
\(=1-\dfrac{1}{4}=\dfrac{3}{4}\)

Chọn D.
Ta có : sin2a = 2.sina. cosa và sin2a = 1 - cos2a.
Do đó;
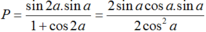
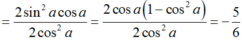

a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}\)
Lại có: \(\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}\)
\(\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0\)
Lại có: \(\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}\)
\(\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
Ta có: \(\sin {75^o} = \cos\left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}\); \(\sin {55^o} = \cos\left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}\)
\(\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
Ta có: \(\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}\)
Mà: \(\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}\)
\(\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.(-\cot {25^o})\\ \Leftrightarrow D =- \tan {45^o} = -1\end{array}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Ta có: \(\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}\)
Mà: \(\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}\Rightarrow \cot {100^o} =- \tan {10^o}\)
\(\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.(-\tan {10^o})\\ \Leftrightarrow E = -\cot {30^o} =- \sqrt 3 .\end{array}\)

\(B=cos^2x+sin^2x+tan^2x\)
\(=1+tan^2x\)
\(=\dfrac{1}{cos^2x}=1:\dfrac{1}{4}=4\)

Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
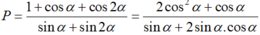
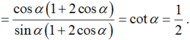


\(A=cos\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\left(-cos\left(\pi-\dfrac{5\pi}{7}\right)\right)=-cos\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(\Rightarrow A.sin\left(\dfrac{\pi}{7}\right)=-sin\left(\dfrac{\pi}{7}\right).cos\left(\dfrac{\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=-\dfrac{1}{2}sin\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{2\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)=-\dfrac{1}{4}sin\left(\dfrac{4\pi}{7}\right)cos\left(\dfrac{4\pi}{7}\right)\)
\(=-\dfrac{1}{8}sin\left(\dfrac{8\pi}{7}\right)=\dfrac{1}{8}sin\left(\dfrac{\pi}{7}\right)\)
\(\Rightarrow A=\dfrac{1}{8}\)
\(B=\dfrac{\sqrt{3}}{2}.cos48^0.cos24^0.cos12^0\)
\(\Rightarrow B.sin12^0=\dfrac{\sqrt{3}}{2}sin12^0.cos12^0cos24^0.cos48^0\)
\(=\dfrac{\sqrt{3}}{4}sin24^0cos24^0cos48^0=\dfrac{\sqrt{3}}{8}sin48^0.cos48^0\)
\(=\dfrac{\sqrt{3}}{16}sin96^0=\dfrac{\sqrt{3}}{16}cos6^0\)
\(\Rightarrow2B.sin6^0.cos6^0=\dfrac{\sqrt{3}}{16}cos6^0\Rightarrow B=\dfrac{\sqrt{3}}{32.sin6^0}\)
Biểu thức này ko thể rút gọn tiếp được
\(P=cos20+cos160+cos40+cos140+...+cos80+cos100+cos180\)
\(=2cos90.cos70+2cos90.cos50+...+2cos90.cos10+cos180\)
\(=cos90\left(2cos70+2cos50+...+2cos10\right)+cos180\)
\(=cos180=-1\) (do \(cos90=0\))