Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

trước hết bạn hãy bấm nghiệm của chúng trên máy tính rồi tìm ĐKXĐ nhé !
b = 1 =>b2=b
=> A = \(\sqrt{a^2+4ab+4b^2}-\sqrt{4a^2-12ab+9b^2}\)
= \(\sqrt{\left(a+2b\right)^2}-\sqrt{\left(2a-3b\right)^2}\)
= \(\sqrt{\left(\sqrt{2}+2\right)^2}-\sqrt{\left(2\sqrt{2}-3\right)^2}\)
= \(\sqrt{2}+2-3+2\sqrt{2}\)
= \(3\sqrt{2}-1\)

2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)

Đáp án đúng : A
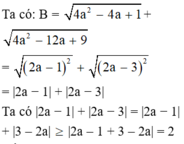
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2

Áp dụng BĐT \(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(a+c-b\right)\)
\(\Leftrightarrow abc\ge\left(3-2a\right)\left(3-2b\right)\left(3-2c\right)\ge0\)
\(\Leftrightarrow9abc+18\left(a+b+c\right)\ge12\left(ab+bc+ca\right)+27\)
\(\Leftrightarrow abc\ge\dfrac{4}{3}\left(ab+bc+ca\right)-3\)
Do đó:
\(P=4a^2+4b^2+4c^2+abc\ge4a^2+4b^2+4c^2+\dfrac{4}{3}\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{2}{3}\left(a+b+c\right)^2+\dfrac{10}{3}\left(a^2+b^2+c^2\right)-3\)
\(P\ge\dfrac{2}{3}\left(a+b+c\right)^2+\dfrac{10}{9}\left(a+b+c\right)^2-3=13\)
Đề bài bạn viết thiếu số 1 bên vế phải rồi
Lời giải:
Áp dụng BĐT Schur:
$abc\geq (a+b-c)(b+c-a)(c+a-b)=(3-2a)(3-2b)(3-2c)$
$\Leftrightarrow 9abc\geq 12(ab+bc+ac)-27$
$\Leftrightarrow abc\geq \frac{4}{3}(ab+bc+ac)-3$
Do đó:
$4(a^2+b^2+c^2)+abc\geq 4(a^2+b^2+c^2)+\frac{4}{3}(ab+bc+ac)-3$
$=\frac{10}{3}(a^2+b^2+c^2)+\frac{2}{3}(a+b+c)^2-3$
$\geq \frac{10}{9}(a+b+c)^2+\frac{2}{3}(a+b+c)^2-3=13$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=1$

Áp dụng BĐT sờ vác sơ,ta có:
\(P\ge\frac{4}{a+b}\ge\frac{4}{2\sqrt{2}}=\sqrt{2}\)
Dấu "="xảy ra khi \(a=b=\sqrt{2}\)
Ngoài ra bạn có thể dùng BCS,BĐT phụ 1/x+1/y>=4/x+y,...

\(A=\frac{2a-3\sqrt{a}-2}{\sqrt{a}-2}\\ =\frac{2a-4\sqrt{a}+\sqrt{a}-2}{\sqrt{a}-2}\\ =\frac{\left(2\sqrt{a}+1\right)\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\\ =2\sqrt{a}+1\)
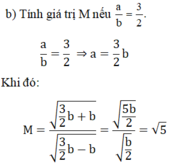
Bạn rút gọn biểu thức trên đi
rồi thay a = căn 2 , b= 1 vào cái biểu thức mà bạn vừa rút gọn là ra kết quả cuối cùng ngay mà