Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 1 cạnh góc vuông là x (cm; x>0).
Thì cạnh góc vuông còn lại là (x +14) cm.
Theo định lý Pytago ta có: x2 + (x +14)2 = 262.
ó x2 + x2 + 28x + 142 = 262
ó2x2 + 28x – 480 = 0
ó x2 + 14x – 240 = 0
ó x2 + 24x – 10x – 240 =0
ó x (x + 24) – 10 (x + 24) = 0
ó (x – 10) (x + 24) = 0
ó x − 10 = 0 x + 24 = 0 ó x = 10 ( t m ) x = − 24 ( k t m )
Suy ra hai cạnh góc vuông của tam giác là 10 cm; 10 +14 = 24 cm.
Chu vi tam giác vuông là 10 + 24 + 26 = 60 cm.
Đáp án cần chọn là: C

Gọi độ dài của hai cạnh góc vuông lần lượt là x và y. (Điều kiện: x, y > 0)
Theo đề bài ta có: x 2 + y 2 = 13 2 = 169 x + y = 17
Từ đó tính được (x, y) = (5, 12) hoặc (12,5)
Þ Diện tích tamgiacs đó là: S = 30cm2

Gọi 2 cạnh tam giác là x và x+2
Áp dụng định lý pytago , ta có :
x2 + (x+2)2 = 102
\(=>\) x2+x2+4x+4=100
\(=>\) x=6 ( Vì x > 0 )
\(=>\) 2 cạnh góc vuông là 6cm và 8cm
\(=>\) S=6.8:2=24cm2

Gọi 2 cạnh góc vuông và cạnh huyền lần lượt là a, b và c
Áp dụng định lí Pi-ta-go, ta có: \(a^2+b^2=c^2=169\)
Mặt khác a+b=17\(\Rightarrow\left(a+b\right)^2=289\Leftrightarrow a^2+b^2+2ab=289\Leftrightarrow169+2ab=289\Rightarrow ab=60\)
\(\Rightarrow S_{\Delta}=\frac{ab}{2}=\frac{60}{2}=30\)

Gọi 2 cạnh góc vuông là a, b (cm; a,b >0)
Ta có: \(\left\{{}\begin{matrix}a+b=17\left(1\right)\\a^2+b^2=13^2=169\left(Pytago\right)\left(2\right)\end{matrix}\right.\)
(1) <=> (a+b)2 = 289
<=> 2ab = 120
<=> ab = 60
<=> \(S=\dfrac{ab}{2}=\dfrac{60}{2}=30\left(cm^2\right)\)

Đặt độ dài 2 cạnh góc vuông của tam giác đó là a và b; độ dài cạnh huyền là c (a,b,c > 0)
Diện tích của tam giác đó là \(\frac{ab}{2}=14\)(cm2) \(\Rightarrow ab=28\Leftrightarrow2ab=56\)(1)
Áp dụng ĐL Pytago ta có: \(a^2+b^2=c^2=13^2=169\)(2)
(1) + (2) \(\Rightarrow a^2+2ab+b^2=56+169=225\Leftrightarrow\left(a+b\right)^2=225\)
\(\Leftrightarrow a+b=\sqrt{225}=15\)(cm). Vậy ...

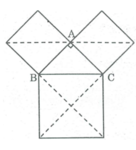
Gọi S là diện tích của tam giác ABC.
Hình vuông có cạnh AB được chia thành hai tam giác vuông cân bằng △ ABC nên diện tích hình vuông cạnh AB bằng 2S.
Hình vuông có cạnh AC được chia thành hai tam giác vuông cân bằng △ ABC nên diện tích hình vuông cạnh AC bằng 2S.
Hình vuông cạnh BC được chia thành bốn hình tam giác vuông cân bằng △ ABC nên có diện tích bằng 4S.
Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.
GỌI 2 cạnh góc vuông của tam giác cân tìm là a và b (a >b >0)
theo bài ra ta có
a - b = 14
vì tam giác đã cho là tam giác vuông theo định là py- ta- go ta có
a2 +b2 =262
(a2 - 2ab + b2) +2ab = 262
(a - b)2 + 2ab = 262 mà a - b =14
142 + 2ab = 262
2ab = 262 - 142
2ab =480
ab = 240
suy ra diện tích tam giác cần tìm là 240 / 2 = 120 (m)
diện tích là 120 m2