Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
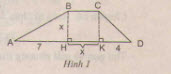
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S = BH(BC+DA)2BH(BC+DA)2
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S = x(11+2x)2x(11+2x)2
2) Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.

Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.

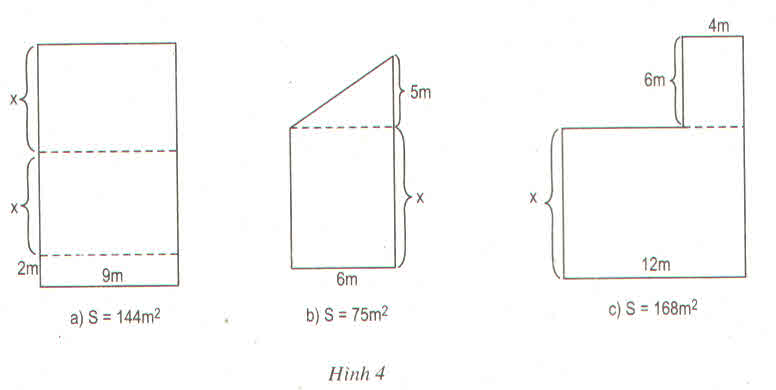
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.

a) Đúng
b)Đúng
c)Sai vì nghiệm không thỏa mãn ĐKXĐ
d)Sai vì có 1 nghiệm không thỏa mãn ĐKXĐ

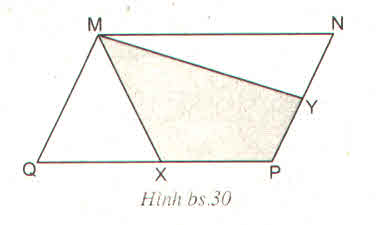
Kẻ đường chéo MP
Ta được SMQX= SMPX
SMNY=SMPY
=> SMXPY= SMPX + SMPY
Khi đó \(S_{MXPY}=\dfrac{1}{2}S\)
Nhớ tick nhé !
Sau khi kẻ đường thẳng MP ta có:
\(\Delta MPQ=\Delta MPN\) (cạnh-cạnh-cạnh)
=> \(\dfrac{1}{2}\)SMPQ = \(\dfrac{1}{2}S_{MPN}\)
hay \(\Delta MPX=\Delta MPY\).
Vì \(S_{MPX}+S_{MPY}=S_{MXPY}=S_{MXQ}+S_{MYN}\) nên SMXPY = \(\dfrac{1}{2}S\).
Vậy SMXPY = \(\dfrac{1}{2}S\).
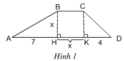
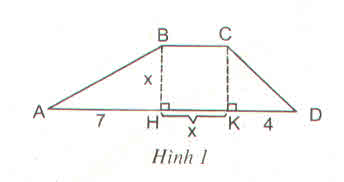

1) Ta có: S = BH x (BC + DA) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2.
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = 1/2.BH.AH = 1/2.7.x = 7x/2.
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = 1/2.CK.KD = 1/2.4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = 7x/2 + x2 + 2x = x2 + 11x/2.
- Với S = 20 ta có phương trình:
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.