Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1) Ta có: S = BH x (BC + DA) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2.
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = 1/2.BH.AH = 1/2.7.x = 7x/2.
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = 1/2.CK.KD = 1/2.4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = 7x/2 + x2 + 2x = x2 + 11x/2.
- Với S = 20 ta có phương trình:
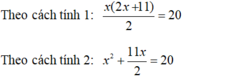
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
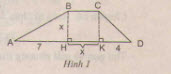
Hướng dẫn giải:
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S =
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S =
2) Ta có: S = SABH + SBCKH + SCKD.
= .AH.BH + BH.HK + CK.KD
= .7x + x.x + x.4
= x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
= 20 (1)
x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.
a) Phương trình bậc nhất một ẩn là phương trình 2x -8 = 0
b) Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = {-2/3}
a) Phương trình bậc nhất một ẩn là phương trình :
2x - 8 = 0
b) Hai phương trình tương đương với nhau vì chúng có cùng tập nghiệm
Hai PT đã cho tương đương với nhau vì chúng có cùng tập nghiệm
S = ( -2 / 3 )
ai tk mk mk tk lại!!
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
a, Để phương trình (1) là phương trình bậc nhất một ẩn thì \(m-1\ne0\Leftrightarrow m\ne1\)
\(b,2x+5=3\left(x+2\right)-1\\ \Leftrightarrow2x+5=3x+6-1\\ \Leftrightarrow2x+5=3x+5\\ \Leftrightarrow x=0\)
b,Để pt trên là pt tương đương thì pt(1) có nghiệm x=0, thay x=0 vào pt(1) ta có:
\(2\left(m-1\right)x+3=2m-5\\ \Leftrightarrow2\left(m-1\right).3+3=2m-5\\ \Leftrightarrow2m-5=3\\ \Leftrightarrow2m=8\\ \Leftrightarrow m=4\)
a: Để (1) là phươg trình bậc nhất 1 ẩn thì (m-1)<>0
hay m<>1
b: Ta có: 2x+5=3(x+2)-1
=>2x+5=3x+6-1
=>3x+5=2x+5
=>x=0
Thay x=0 vào (1), ta được:
2m-5=3
hay m=4
a.
(1) là pt bậc nhất 1 ẩn khi và chỉ khi \(2\left(m-1\right)\ne0\Leftrightarrow m\ne1\)
b.
Ta có: \(2x+5=3\left(x+2\right)-1\)
\(\Leftrightarrow2x+5=3x+5\)
\(\Leftrightarrow x=0\)
Do đó (1) tương đương (*) khi (1) nhận \(x=0\) là nghiệm
\(\Rightarrow2\left(m-1\right).0+3=2m-5\)
\(\Rightarrow m=4\)
a, Để pt trên là pt bậc nhất 1 ẩn thì: \(m-1\ne0\Leftrightarrow m\ne1\)
\(b,2x+5=3\left(x+2\right)-1\\ \Leftrightarrow2x+5=3x+6-1\\ \Leftrightarrow2x+5=3x+5\\ \Leftrightarrow x=0\)
Để pt (1) tương đương vs pt trên thì
\(2\left(m-1\right).0+3=2m-5\\ \Leftrightarrow2m-5=3\\ \Leftrightarrow2m=8\\ \Leftrightarrow m=4\)
a, để pt trên là pt bậc nhất khi m khác 2
b, Ta có \(2x+5=x+7-1\Leftrightarrow x=1\)
Thay x = 1 vào pt (1) ta được
\(2\left(m-2\right)+3=m-5\Leftrightarrow2m-1=m-5\Leftrightarrow m=-4\)
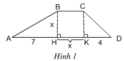
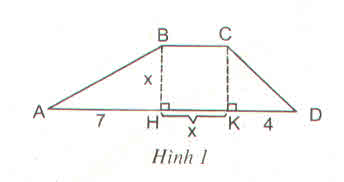
Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.