Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hình thoi ABCD có cạnh AB = 6cm, ∠A = 600

+ ABCD là hình thoi ⇒ ΔBAD cân tại A. Mà ∠A = 600 nên ΔABD là tam giác đều ⇒ BD = AB = 6cm
+ AC ⊥ BD và BI = ID = 3cm
Trong tam giác vuông AIB áp dụng định lý pitago
AI2 = AB2 – IB2 = 36 – 9 = 27 ⇒ AI = √27 (cm)
Suy ra: AC = 2AI = 2√27 (cm)
Vậy SABCD = 1/2AC.BD = 1/2.2√27 .6 = 12√27 (cm2)

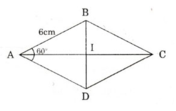
Cho hình thoi ABCD có cạnh AB = 6cm, góc ∠A = 60o.
- Cách 1:
ΔABD là tam giác đều nên BD = AB = 6cm
I là giao điểm của AC và BD => AI ⊥ DB
⇒ AI là đường cao của tam giác đều ABD nên
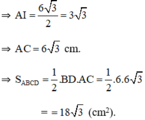
- Cách 2:
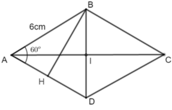
Khi đó ΔABD là tam giác đều. Từ B vẽ BH ⊥ AD thì HA = HD.
Nên tam giác vuông AHB là nửa tam giác đều.
BH là đường cao tam giác đều cạnh 6cm, nên
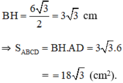

C B A D 7cm 9cm 8cm 30 độ H
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}\).(7+9).4=32 cm2
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}.\left(7+9\right).4\)=32 cm2

2 4 2 45 o A B C D E
Hạ đường cao CE thì EB = AB - AE = AB - DC = 4 - 2 =2.
Tam giác vuông EBC có góc B = 45 độ nên nó là tam giác vuông cân. Suy ra CE = EB = 2.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.CE=\dfrac{4+2}{2}.2=6\left(cm^2\right)\)

câu c nhé
gọi DE giao AC =O, ta có tam giác AEC cân tại E, cậu tự chứng minh
thì góc EAC=gócECA, mà góc ECA=góc CAD ( so le trong)
=> AO là phân giác góc EAD
mặt khác cậu dễ dàng chứng minh DE là trung trực của AC => AO vuông góc với ED
tam giác ADE có phân giác đồng thời là trung tuyến => cân
rồi cậu tự chúng minh tiếp nhé

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

Câu hỏi của Truong Tuan Dat - Toán lớp 8 - Học toán với OnlineMath
Em sai đề rồi nhé! Tham khảo đề bài và bài làm tại link này nhé em
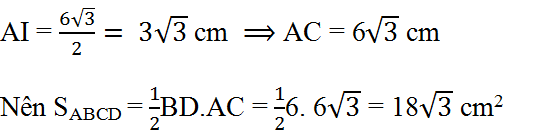


Ta có : AB=BC (ABCD là hình thoi)
=> Tam giác ABC cân tại B
Mà góc B =60o
=> Tam giác ABC đều.
=> AB=BC=CA=6cm
BD=2BE=2.\(\dfrac{\sqrt{3}}{2}\).6=6\(\sqrt{3}\)cm (bạn tự c/m nhé, nó không khó đâu).
SABCD=\(\dfrac{1}{2}\).6.6.\(\sqrt{3}\)=18\(\sqrt{3}\)