Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta kí hiệu S (MNP) là diện tích tam giác MNP
a) Diện tích hình thang ABCD = 1/2 (AB+CD)= 1/2 (50 + 20) . 14 = 245 (cm2)b,S(AED)=S(ACD) - S(ECD) S(BEC) = S(BCD) − S(ECD) mà S(ACD) = S(BCD) nên S(AED) = S(BEC).c, BE/DE = S(AEB) / S(AED) = S(CEB) / S(CED) = S(AEB) + S(CEB) / S(AED) + S(CED) = S(ABC) / S(ACD) = AB / CD = 3/4=> S(CEB) / S(CED) = 3/4 =>S(CEB) + S(CED) / S(CED) = 7/4 => S(DBC) / S(CED) = 7/4 => S(CED) = 4/7 . S(DBC)Ta có S(DBC) = 140 cm² nên S(CED) = 80 cm².
Cao Thái Minh
\(S_{ABD}\)= \(S_{ABC}\) (chung đáy AB, chiều cao bằng chiều cao hình thang).
Mà 2 tam giác này có phần chung ABG nên \(S_{AGD}\) = \(S_{BGC}\)= 18cm2.
Hai tam giác ADG và CDG có chung cạnh đáy DG nên 2 đường cao tỉ lệ với 2 diện tích là 18/25. Hai đường cao của 2 tam giác này cũng là 2 đường cao của 2 tam giác ABG và CBG,
Diện tích tam giác ABG là:
18 : 25 x 18 = 12,96 (cm2)
Diện tích hình thang ABCD là:
18 + 25 + 18 + 12,96 = 73,96 (cm2)
dt_ABD = dt_ABC (chung đáy AB, chiều cao bằng chiều cao hình thang).
Mà 2 tam giác này có phần chung ABG nên dt_AGD = dt_BGC = 18cm2.
Hai tam giác ADG và CDG có chung cạnh đáy DG nên 2 đường cao tỉ lệ với 2 diện tích là 18/25. Hai đường cao của 2 tam giác này cũng là 2 đường cao của 2 tam giác ABG và CBG,
Diện tích tam giác ABG là:
18 : 25 x 18 = 12,96 (cm2)
Diện tích hình thang ABCD là:
18 + 25 + 18 + 12,96 = 73,96 (cm2)
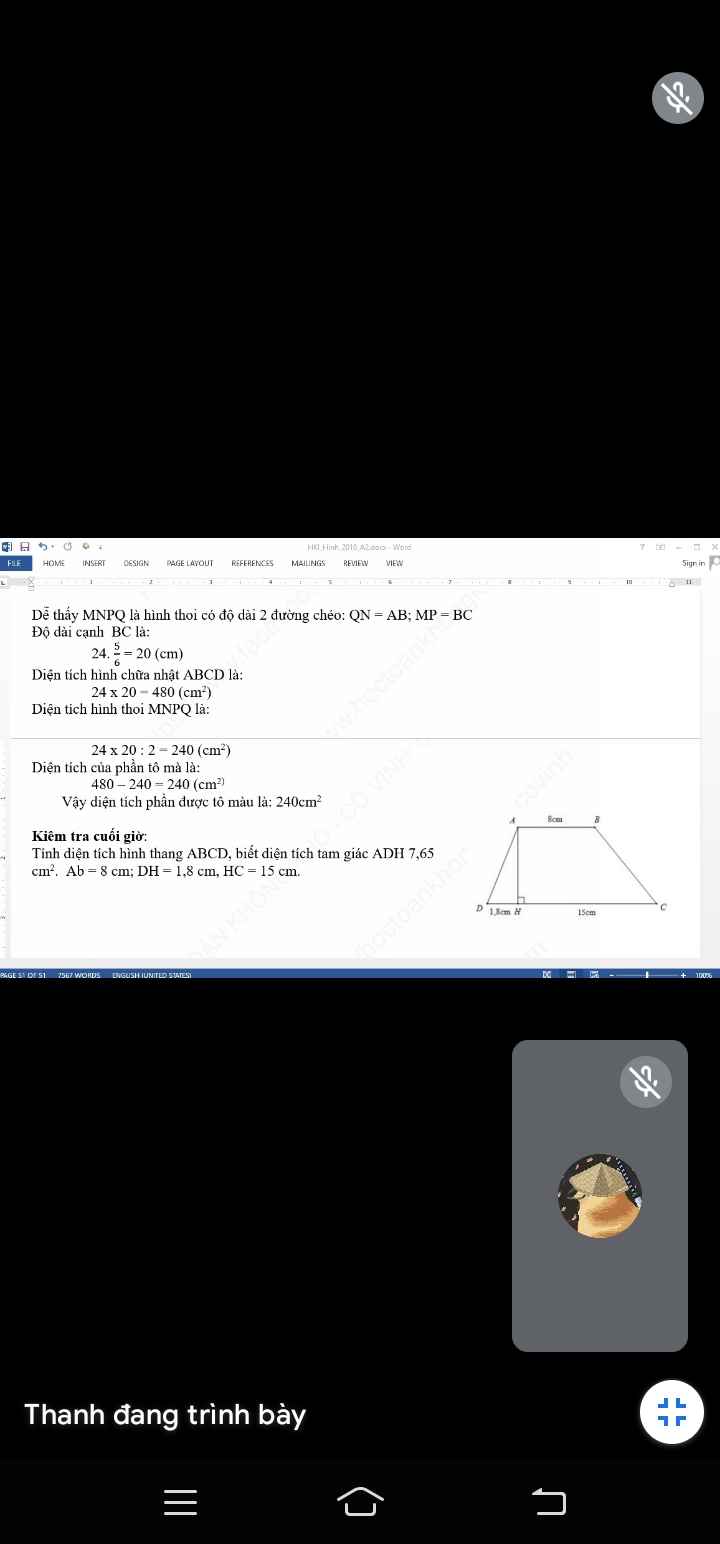
Độ dài đường cao AH: \(\dfrac{2.7,65}{1,8}=8,5\left(cm\right)\)
Độ dài cạnh CD: \(1,8+15=16,8\left(cm\right)\)
Diện tích hình thang: \(\dfrac{1}{2}.8,5.\left(16,8+8\right)=105,4\left(cm^2\right)\)