Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
y = x4 - sin2x
⇒ y’ = 4x3 – 2cos2x ⇒ y’’ = 12x2 + 4sin2x
⇒ y’’’ = 24x + 8cos2x ⇒ y(4) = 24 – 16sin2x
y ' = 2 2 − 3 x 2 x + 1 . 2 − 3 x 2 x + 1 ' = 2 2 − 3 x 2 x + 1 . − 3 2 x + 1 − 2 2 − 3 x 2 x + 1 2 = 2 2 − 3 x 2 x + 1 . − 7 2 x + 1 2 = − 14 2 x + 1 2 . 2 − 3 x 2 x + 1
Chọn đáp án A
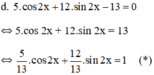
Vì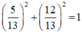 
nên tồn tại α thỏa mãn
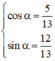
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
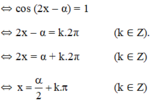
Vậy phương trình có họ nghiệm
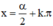(k ∈ Z)
với α thỏa mãn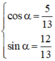 
lim x → π 3 2 sin 2 x + sin x - 1 2 sin 2 x - 3 sin x + 1 = 1 + 3 5 - 3 3
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).
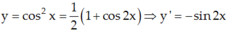
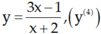
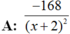
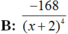
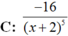
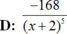
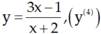
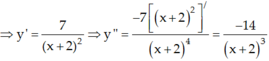
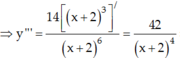
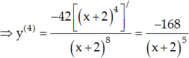
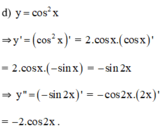
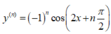
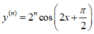
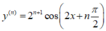
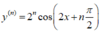
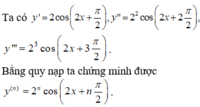
Chọn D.
Có y’ = x’sin2x + x.(sin2x)’ = sin2x + 2xcos2x
⇒ y’’ = (sin2x)’ + (2x)’cos2x + 2x(cos2x)’ = 4cos2x – 4xsin2x
⇒ y’’’ = 4(cos2x)’ – (4x)’sin2x – 4x(sin2x)’ = -8sin2x – 4sin2x – 8cos2x
= -12sin2x – 8cos2x.