Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Có y’ = x’sin2x + x.(sin2x)’ = sin2x + 2xcos2x
⇒ y’’ = (sin2x)’ + (2x)’cos2x + 2x(cos2x)’ = 4cos2x – 4xsin2x
⇒ y’’’ = 4(cos2x)’ – (4x)’sin2x – 4x(sin2x)’ = -8sin2x – 4sin2x – 8cos2x
= -12sin2x – 8cos2x.

\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)

Chọn D
y ' = sin 2 x + cos 2 x / . 2 sin 2 x − cos 2 x − 2 sin 2 x − cos 2 x / . sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2
y ' = 2 cos 2 x − 2 sin 2 x 2 sin 2 x − cos 2 x − 4 cos 2 x + 2 sin 2 x sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2 = 4. c os2x. sin2x - 2cos 2 2 x − 4 sin 2 2 x + 2. sin 2 x . c os2x ( 2 sin 2 x − cos 2 x ) 2 − ( 4cos2x . sin2x + 4cos 2 2 x + 2 sin 2 2 x + 2 sin 2 x . c os2x ( 2 sin 2 x − c os2x) 2
y ' = − 6 cos 2 2 x − 6 sin 2 2 x 2 sin 2 x − cos 2 x 2 = − 6 2 sin 2 x − cos 2 x 2

\(a,y'=3x^2-4x+2\\ \Rightarrow y''=6x-4\\ b,y'=2xe^x+x^2e^x\\ \Rightarrow y''=4xe^x+x^2e^x+2e^x\)

a: \(y=x\cdot e^{2x}\)
=>\(y'=\left(x\cdot e^{2x}\right)'\)
\(=x\cdot\left(e^{2x}\right)'+x'\cdot\left(e^{2x}\right)\)
\(=e^{2x}+2\cdot x\cdot e^{2x}\)
\(y''=\left(e^{2x}+2\cdot x\cdot e^{2x}\right)'\)
\(=\left(e^{2x}\right)'+\left(2\cdot x\cdot e^{2x}\right)'\)
\(=4\cdot e^{2x}+4\cdot x\cdot e^{2x}\)
b: \(y=ln\left(2x+3\right)\)
=>\(y'=\dfrac{\left(2x+3\right)'}{\left(2x+3\right)}=\dfrac{2}{2x+3}\)
=>\(y''=\left(\dfrac{2}{2x+3}\right)'=\dfrac{2\left(2x+3\right)'-2'\left(2x+3\right)}{\left(2x+3\right)^2}\)
\(=\dfrac{4}{\left(2x+3\right)^2}\)
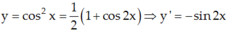
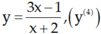
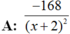
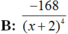
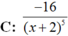
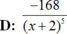
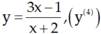
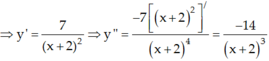
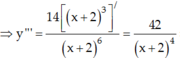
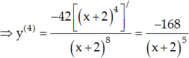
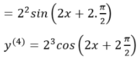
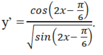
Chọn C.
y = x4 - sin2x
⇒ y’ = 4x3 – 2cos2x ⇒ y’’ = 12x2 + 4sin2x
⇒ y’’’ = 24x + 8cos2x ⇒ y(4) = 24 – 16sin2x