Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình làm câu c thôi ( câu a,b mấy trang khác có nha). Hình mn tự vẽ nha.
Theo b, có: Tam giác DCE là tam giác đều
=> DCE=CDE=DEC=60
Xét tam giác CND:
Áp dụng định lí:" Tổng ba góc một tam giác bằng 180"
=>CND+CDN+DCN=180
=>CND+60+10=180 (vì ICD=10; CDE= 60)
=>CND=180-70=110 (1)
Xét tam giác CNE:
Áp dụng định lí:"Tổng ba góc một tam giác bằng 180"
=>CNE+CEN+NCE=180
=>CNE+60+(ACB+ECF)=180
=>CNE+60+30+20=180
=>CNE+110=180
=>CNE=70 (2)
Từ (1) và (2) suy ra: CND+CNE=70+110=180
=>DNE=180 =>DNE là góc bẹt
=>D; N; E thẳng hàng (ĐPCM)

c) \(\frac{2^{10}\cdot13+2^{10}\cdot65}{2^8\cdot3\cdot13}=\frac{2^{10}\left(13+65\right)}{2^8\cdot3\cdot13}=\frac{2\cdot78}{3\cdot13}=\frac{2\cdot2\cdot3\cdot13}{3\cdot13}=4\)
d) \(\frac{3^{43}+3^4}{3^{39}+3^0}=\frac{3^4\left(3^{39}+1\right)}{3^{39}+1}=3^4=81\)
e) \(\frac{3^{13}\cdot99-15\cdot3^{14}}{3^{15}}=\frac{3^{13}\left(99-15\cdot3\right)}{3^{15}}=\frac{99-45}{3^2}=\frac{54}{3^2}=\frac{2\cdot3^3}{3^2}=\frac{2}{3}\)
f) \(\frac{\left(3\cdot4\cdot2^{16}\right)^2}{11\cdot2^{13}\cdot4^1-16^9}=\frac{3^2\cdot4^2\cdot2^{32}}{11\cdot2^{13}\cdot4-4^{18}}=\frac{3^2\cdot4^2\cdot2^{32}}{4\left(11\cdot2^{13}-2^{34}\right)}=\frac{3^2\cdot2^{34}}{2^{13}\left(11-2^{21}\right)}=\frac{3^2\cdot2^{21}}{11-2^{21}}\)
c) \(\frac{2^{10}\cdot13+2^{10}\cdot65}{2^8\cdot3\cdot13}\)
\(=\frac{2^{10}\left(13+65\right)}{2^8\cdot3\cdot13}\)(có chung 2^10 nên đặt ra ngoài)
\(=\frac{2^8\cdot2^2\cdot78}{2^8\cdot3\cdot13}\) (vì 2^10 = 2^8 * 2^2. còn 78 là tổng của 2 số hạng trong ngoặc)
\(=\frac{2^2\cdot78}{3\cdot13}\)(chỗ này đoạn trên nhầm, phải là 2^2 mới đúng. Trên, dưới cùng có 2^8 và là phép nhân nên triệt tiêu)
\(=\frac{2^2\cdot3\cdot13}{3\cdot13}\) (phân tích 78 ra thừa số nguyên tố ta được 3*13 )
\(=4\) (tử và mẫu cùng có 3*13 và là phép tình nhân nên đc triệt tiêu. Còn lại 2^2 . mà 2^2 =4 nên kq là 4)
Chú ý: trong bài làm ko ghi lại phần trong ngoặc

câu a: có 2 bước
bước 1 : tính cạnh BH
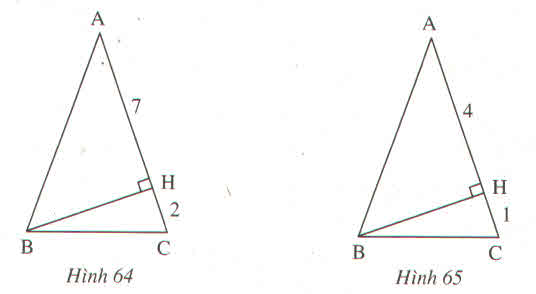
ta có: AB = AC = 7 +2 =9
theo định lý Py -ta -go:
ta có : BH2 = AB2- HB2
BH2= 92-72
=>BH=\(\sqrt{32}\)
bước 2: tính cạnh BC
theo định lí Py-ta-go
ta có: BH2 + HC2=BC2
=>BC2= \(\sqrt{32}\)2 + 22 =36
=> BC = \(\sqrt{36}\) = 6
câu b: có 2 bước
bước 1: tìm cạnh BH
ta có AB = AC= 4+1=5
theo định lí Py-ta-go
ta có BH2 = AB2 - AH2
BH2 = 52-42
=> BH= 3
bước 2 : tìm cạnh BC
theo định lí Py-ta-go
ta có : BC2= HC2+BH2
BC2= 12+32
=>BC=\(\sqrt{10}\)
a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC =7 + 2 = 9 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go,ta có:
AB2 = BH2 + AH2
\(\Rightarrow\)92 = BH2 + 72
BH2 = 92 - 72
BH2 = 81 - 49
BH2 = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = BH2 + HC2
\(\Rightarrow\)BC2 = \(\sqrt[]{32}\)2 + 22
BC2 = 32 + 4
BC2 = 36\(\Rightarrow\)BC = 6 (cm)
b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC = 4 + 1 = 5 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go, ta có:
AB2 = HB2 + AH2
\(\Rightarrow\)52 = HB2 + 42
HB2 = 52 - 42
HB2 = 25 - 16
HB2 = 9 \(\Rightarrow\)HB = 3 (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = HC2 + BH2
\(\Rightarrow\)BC2 = 12 + 32
BC2 = 1 + 9
BC2 = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)

Ta có: trên nửa mặt phẳng bờ AB có chứa điểm G, có tam giác ABD. Nối D với F Ta có:
Góc FBA= góc ABC-góc FBC Góc ABC =(1800 - BAC)/2=1400 :2=700
=> góc FBC=góc EBA=300 => FBA= 700 -300 =400
=>góc FBA= góc BAI=400 =>tam giác AFB cân tại F
=>FA=FB
Xét tam giác BDF và tam giác ADF có:
DF cạnh chung
FB=FA
BD=AD
=>tam giác BDF= tam giác ADF(c-c-c)
=>góc ADF= góc BDF = góc ABD/2= 300 Mà góc EBA= 30 0
=>góc ADF= góc ABE=300
Ta có tam giác ABC cân tại A co AH là đường cao =>AD la p.giác của tam giác ABC
=>góc BAH= góc CAH=góc BAC/2=200 => góc DAF= góc BAE=200
Xét tam giác BAE và tam giác DAI có
Góc DAI= góc BAD
AB=AD
Góc ADF= góc ABD
=>tam giác BAD = tam giác DAF(g-c-g)
=>AE=AF ( cặp cạnh tương ứng)