Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại x = 1/2 ta có: 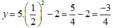
Vậy 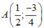 thuộc đồ thị hàm số
thuộc đồ thị hàm số
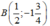 không thuộc đồ thị hàm số.
không thuộc đồ thị hàm số.
Tại x = 2 thì y = 5.22 – 2 = 18.
Vậy điểm C(2; 18) thuộc đồ thị hàm số.

Ta có: \(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\)
\(\Rightarrow\frac{abc}{c\left(a+b\right)}=\frac{abc}{a\left(b+c\right)}=\frac{abc}{b\left(c+a\right)}\)
\(\Rightarrow c\left(a+b\right)=a\left(b+c\right)=b\left(c+a\right)\)
\(\Rightarrow ac+bc=ab+ac=bc+ab\)
Lại có: \(ac+bc=ab+ac\)\(\Rightarrow bc=ab\)\(\Rightarrow a=c\) (1)
\(ab+ac=bc+ab\)\(\Rightarrow ac=bc\)\(\Rightarrow a=b\) (2)
Từ (1) và (2) \(\Rightarrow a=b=c\)
Ta có: \(P=\frac{ab^2+bc^2+ca^2}{a^3+b^3+c^3}=\frac{a.a^2+b.b^2+c.c^2}{a^3+b^3+c^3}=\frac{a^3+b^3+c^3}{a^3+b^3+c^3}=1\)

Áp dụng ĐL Pi ta go trong tam giác vuông AOH có: OA2 = AH2 + AH2 = 32 + 52 = 34 => AO = \(\sqrt{34}\)
Hình mình vẽ giống bạn Trần Thị Loan nhưng lời giải thì thế này:
Áp dụng ĐL Pi ta go vào tam giác vuông AHO vuông ở H ta có
OA2=HA2=HO2
Hay OA2=52+32
OA2= 25+9=34
=> OA=\(\sqrt{34}\)
=> OA= -\(\sqrt{34}\)( loại)
Vậy.................

Câu 2. Trong các biểu thức sau, biểu thức nào là biểu thức đại số:
A. (34 – 5) : 8 B. (x + y)2 C. x2 + 2x + 1 D. Cả 3 đáp án trên

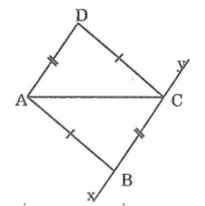
Nối AB, nửa mặt phẳng bờ BC có chứa A. Vẽ cung tròn tâm A bán kính bằng BC. Vẽ cung tròn tâm C bán kính bằng AB. Hai cung tròn cắt nhau tại D.
Kẻ đường thẳng AD ta có AD // xy

a)Xét tam giác AOD VÀ COB có AO=OC ,OB=OD ,chung góc O=> tam giác AOD =tam giác COB(cgc)=>AD=BC
b) Ta có OA=OC,OB=OC=> AB=CD.
Tam giác AOD=tg COB=> góc OAD =góc BCO góc
Và ADO=gócCBO(2 góc tương ứng).
Mà góc ABI + góc CBO=180 độ(kề bù)
góc CDI+góc ADO=180 độ (kề bù)
=> Góc CBO=ADO
Xét tg ABI và tg CDI có AB= CD(cm trên),gics CBO= góc ADO,góc OAC= BCO=> tg ABI=th CDI => AI=CI,BI=Di
c) \(\frac{2^{10}\cdot13+2^{10}\cdot65}{2^8\cdot3\cdot13}=\frac{2^{10}\left(13+65\right)}{2^8\cdot3\cdot13}=\frac{2\cdot78}{3\cdot13}=\frac{2\cdot2\cdot3\cdot13}{3\cdot13}=4\)
d) \(\frac{3^{43}+3^4}{3^{39}+3^0}=\frac{3^4\left(3^{39}+1\right)}{3^{39}+1}=3^4=81\)
e) \(\frac{3^{13}\cdot99-15\cdot3^{14}}{3^{15}}=\frac{3^{13}\left(99-15\cdot3\right)}{3^{15}}=\frac{99-45}{3^2}=\frac{54}{3^2}=\frac{2\cdot3^3}{3^2}=\frac{2}{3}\)
f) \(\frac{\left(3\cdot4\cdot2^{16}\right)^2}{11\cdot2^{13}\cdot4^1-16^9}=\frac{3^2\cdot4^2\cdot2^{32}}{11\cdot2^{13}\cdot4-4^{18}}=\frac{3^2\cdot4^2\cdot2^{32}}{4\left(11\cdot2^{13}-2^{34}\right)}=\frac{3^2\cdot2^{34}}{2^{13}\left(11-2^{21}\right)}=\frac{3^2\cdot2^{21}}{11-2^{21}}\)
c) \(\frac{2^{10}\cdot13+2^{10}\cdot65}{2^8\cdot3\cdot13}\)
\(=\frac{2^{10}\left(13+65\right)}{2^8\cdot3\cdot13}\)(có chung 2^10 nên đặt ra ngoài)
\(=\frac{2^8\cdot2^2\cdot78}{2^8\cdot3\cdot13}\) (vì 2^10 = 2^8 * 2^2. còn 78 là tổng của 2 số hạng trong ngoặc)
\(=\frac{2^2\cdot78}{3\cdot13}\)(chỗ này đoạn trên nhầm, phải là 2^2 mới đúng. Trên, dưới cùng có 2^8 và là phép nhân nên triệt tiêu)
\(=\frac{2^2\cdot3\cdot13}{3\cdot13}\) (phân tích 78 ra thừa số nguyên tố ta được 3*13 )
\(=4\) (tử và mẫu cùng có 3*13 và là phép tình nhân nên đc triệt tiêu. Còn lại 2^2 . mà 2^2 =4 nên kq là 4)
Chú ý: trong bài làm ko ghi lại phần trong ngoặc