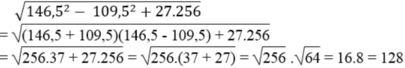NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
1
22 tháng 6 2019
\(a,\sqrt{52}.\sqrt{13}=\sqrt{2^2.13}.\sqrt{13}\)
\(=2\sqrt{13}.\sqrt{13}=2.13=26\)
\(b,\sqrt{146,5^2-109,5^2}+27.256\)
\(=\sqrt{\left(146,6-109,5\right)\left(146,5+109,5\right)}+27.256\)
\(=\sqrt{37.256}+27.256\)
\(=\sqrt{4^2.37}+27.16=4\sqrt{37}+4.4.27\)
\(=4\left(\sqrt{37}+108\right)\)
20 tháng 8 2023
a: \(13\sqrt{11}=\sqrt{13^2\cdot11}=\sqrt{1859}\)
b: \(-8\sqrt{2}=-\sqrt{64\cdot2}=-\sqrt{128}\)
c: \(a\sqrt{5a}=\sqrt{a^2\cdot5a}=\sqrt{5a^3}\)
d: \(b\sqrt{\dfrac{5}{ab}}=-\sqrt{b^2\cdot\dfrac{5}{ab}}=-\sqrt{\dfrac{5b}{a}}\)
NV
3
KT
30 tháng 7 2018
Ta có:
\(\left(\sqrt{x^2-6x+13}-\sqrt{x^2-6x+10}\right)\left(\sqrt{x^2-6x+13}+\sqrt{x^2-6x+10}\right)\)
\(=x^2-6x+13-\left(x^2-6x+10\right)\)
\(=3\)
mà \(\sqrt{x^2-6x+13}-\sqrt{x^2-6x+10}=1\)
=> \(\sqrt{x^2-6x+13}+\sqrt{x^2-6x+10}=3\)
31 tháng 7 2018
Em chưa hiểu ở dòng thứ 3,chị có thể giải thích cho em với được ko ạ
23 tháng 8 2019
c) Bình phương hai vế ta được 2015+2017+2\(\sqrt{2015\times2017}\) và 4\(\times\)2016
Ta có 2015 + 2017 + 2\(\sqrt{2015\times2017}\)
= (2016-1) + (2016+1) + 2\(\sqrt{2015\times2017}\)
= 2016 + 2016 + 1 - 1 + 2\(\sqrt{2015\times2017}\)
= 2\(\times\)2016 + 2\(\sqrt{2015\times2017}\) (1)
ta thấy 2015 \(\times\) 2017 =(2016-1) \(\times\) (2016+1)= 20162 - 1
nên (1) \(\Leftrightarrow\)2\(\times\)2016 + 2\(\sqrt{2016^2-1}\)
Ta có 4\(\times\)2016=2\(\times\)2016 + 2\(\times\)2016=2\(\times\)2016 + 2\(\sqrt{2016^2}\)
Vì 20162-1 < 20162 nên 2\(\sqrt{2016^2-1}\) < 2\(\sqrt{2016^2}\)
\(\Leftrightarrow\) 2\(\times\)2016 + 2\(\sqrt{2016^2-1}\) < 2\(\times\)2016 + 2\(\sqrt{2016^2}\)
\(\Leftrightarrow\)2015+2017+2\(\sqrt{2015\times2017}\) < 4\(\times\)2016
Hay \(\sqrt{2015}+\sqrt{2017}\) < \(2\sqrt{2016}\)
23 tháng 8 2019
a) Bình phương hai vế ta được 5+7+\(2\sqrt{5\times7}\) và 13.
Ta có 5+7+\(2\sqrt{5\times7}\) =12+\(2\sqrt{35}\)
13=12+1=12+\(2\times\frac{1}{2}\) =12+\(2\sqrt{\frac{1}{4}}\)
Vì 35 > \(\frac{1}{4}\) nên \(\sqrt{35}\) > \(\sqrt{\frac{1}{4}}\) \(\Leftrightarrow\)2\(\sqrt{35}\) > \(2\sqrt{\frac{1}{4}}\) \(\Leftrightarrow\)12+2\(\sqrt{35}\) > 12+\(2\sqrt{\frac{1}{4}}\)
Hay\(\sqrt{5}\)+\(\sqrt{7}\) > \(\sqrt{13}\)