SY
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
5 tháng 3 2019
4 6 . 9 5 + 6 9 . 120 8 4 . 3 12 − 6 11 = 2 2 6 . 3 2 5 + 2 9 .3 9 .2 3 .3.5 2 3 4 .3 12 − 2 11 .3 11 = 2 12 .3 10 + 2 12 .3 10 .5 2 12 .3 12 − 2 11 .3 11 = 2 12 .3 10 1 + 5 2 11 .3 11 2.3 − 1 = 2.6 3.5 = 4 5
SY
1
10 tháng 4 2016
\(A=\frac{2^{19}3^9+5.2^{18}3^9}{3^9.2^9.2^{10}+3^{10}4^{10}}=\frac{3^9\left(2^{19}+5.2^{18}\right)}{3^92^{19}+3^{10}2^{20}}=\frac{3^9\left(2^{19}+5.2^{18}\right)}{3^9\left(2^{19}+3.2^{20}\right)}=\frac{2^{19}+5.2^{18}}{2^{19}+3.2^{20}}=\frac{2^{18}\left(2+5\right)}{2^{18}\left(2+3.2^2\right)}\)
\(=\frac{2+5}{2+3.2^2}=\frac{7}{14}=\frac{1}{2}\)
22 tháng 3 2020
Đây là bài toán tổng hiệu,đã có tổng của cả P(x) và Q(x) nên\(P\left(x\right)=\frac{x^2+1+2x}{2}=\frac{\left(x^2+x\right)+\left(x+1\right)}{2}=\frac{\left(x+1\right)^2}{2}\)
\(Q\left(x\right)=P\left(x\right)-2x=\frac{\left(x+1\right)^2}{2}-2x=\frac{x^2+2x+1-4x}{2}=\frac{x^2-2x+1}{2}=\frac{\left(x-1\right)^2}{2}\)
Nếu bn hỏi x^2-2x+1 sao lại =(x-1)^2 thì ph giống như (x+1)^2 nhé.
TN
1
2 tháng 1 2017
Gọi d là ƯCLN(a2, a+ b)
=> a2 chia hết cho d
a + b chia hết cho d => a ( a +b) chia hết cho d hay a2 + ab chia hết cho d.
=> a2 + ab - a2 chia hết cho d
=> ab chia hết cho d; mà a, b là hai số nguyên tố cùng nhau (a,b) = 1
=> a chia hết cho d hoặc b chia hêt cho d.
- Nếu a chia hết cho d: Ta có: a + b chia hết cho d => b chia hết cho d
=> d\(\in\) ƯC (a;b) mà \(ƯCLN\)(a , b) =1 => d = 1 =>\(ƯCLN\)(a2, a + b) =1
- Nếu b chia hết cho d: Ta có a + b chia hết cho d => a chia hết cho d
=> d\(\in\) ƯC (a;b) mà \(ƯCLN\)(a , b) =1 => d = 1 =>\(ƯCLN\)(a2, a + b) =1
Vậy (a2, a + b) =1
5 tháng 11 2017
2 , 5 - x = 1 , 3
x = 2 , 5 - 1 , 3
x = 1 , 2
Chúc bạn chăm ngoan học giỏi !
CN
5
PL
4 tháng 11 2016
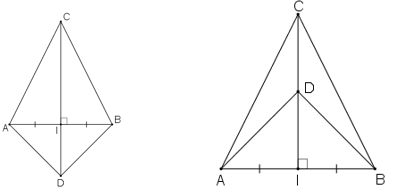
Xét tam giác ACI và tam giác BCI , có
CI là cạnh chung
AC = BC
AI= BI
=> tam giác ACI = tam giác BCI
Xét tam giác ACD và tam giác BCD , có
CD là cạnh chung
AD = BD
AC =BC
=> tam giác ACD = tam giác BCD
Xét tam giác ADI và tam giác BDI , có
DI là cạnh chung
AD = BD
AI = BI
=> tam giác ADI = tam giác BDI
ok 3 cặp nha thư
3 tháng 12 2021
Có hai trường hợp:
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung
2 tháng 1 2018
A=1+3/2^3+4/2^4+5/2^5+...100/2^100
1/2*A = 1/2 + 3/2^4 + 4/2^5 +....+ 99/2^100 + 100/2^101
A- A/2 = 1/2A =1/2 + 3/2^3 + 1/2^4 +...+1/2^100 - 100/2^101
= [1/2+1/2^2 +1/2^3 +...+1/2^100] -100/2^101 (Do 3/2^3 = 1/2^2 +1/2^3)
=[1-(1/2)^101]/(1-1/2) -100/2^101
=(2^101 -1)/2^100 - 100/2^101
=> A = (2^101 -1)/2^99 - 100/2^100
KH
2 tháng 1 2018
Bạn ơi khó hiểu quá bạn giải chi tiết hơn giúp mình nhé mình sẽ k cho bạn 2 cái nhé