
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



i) xy - 6y + 2x - 12
= (xy - 6y) + (2x - 12)
= y(x - 6) + 2(x - 6)
= (x - 6)(y + 2)
ii) 2x(y - z) + (z - y)(x + y)
= 2x(y - z) - (y - z)(x + y)
= (y - z)(2x - x - y)
= (y - z)(x - y)
b) x + 3 = (x + 3)2 ⇔ (x + 3)2 - (x + 3) = 0 ⇔ (x + 3)(x + 3 - 1) = 0
⇔ (x + 3)(x + 2) = 0
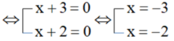
Vậy x = -3; x = -2

A = 5x² + 2y² + 6xy + 2x + 6y + 32
⇒ 2A = 10x² + 4y² + 12xy + 4x + 12y + 64
= (4y² + 12xy + 9x²) + x² + 4x + 12y + 64
= (2y + 3x)² + x² - 14x + 18x + 12y + 9 + 49 + 6
= (3x + 2y)² + (18x + 12y) + 9 + (x² - 14x + 49) + 6
= [ (3x + 2y)² + 6(3x + 2y) + 9 ] + (x - 7)² + 6
= (3x + 2y + 3)² + (x - 7)² + 6.
Do (3x + 2y + 3)² ≥ 0; (x - 7)² ≥ 0 ⇒ (3x + 2y + 3)² + (x - 7)² ≥ 0.
⇒ 2A = (3x + 2y + 3)² + (x - 7)² + 6 ≥ 6
⇒ A ≥ 3. Dấu ''='' xảy ra ⇔ (x - 7)² = 0 và (3x + 2y + 3)² = 0
⇔ x - 7 = 0 và 3x + 2y + 3 = 0
⇔ x = 7 và 2y = -3x - 3 = -3.7 - 3 = -24
⇔ x = 7 và y = -12. Vậy GTNN của A = 3 đạt được ⇔ x = 7 và y = -12.
Nguồn: https://vn.answers.yahoo.com/

`A=-(x^2-2x)-(y^2+6y)+9`
`=-(x^2-2x+1)-(y^2+6y+9)+19`
`=-(x-1)^2-(y+3)^2+19<=19`
Dấu "=" xảy ra khi `x=1` và `y=-3`
`B=-(2x-5)^2+6|2x+5|+4`
`=-[(2x-5)^2-6|2x-5|+9]+13`
`=-(|2x-5|-3)^2+13<=13`
Dấu "=" xảy ra khi `|2x-5|=3<=>[(x=4),(x=1):}`

b: Ta có: \(B=-x^2-y^2+2x-6y+9\)
\(=-\left(x^2-2x+y^2+6y-9\right)\)
\(=-\left(x^2-2x+1+y^2+6y+9-19\right)\)
\(=-\left(x-1\right)^2-\left(y+3\right)^2+19\le19\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-3

\(D=x^2+4y^2-2xy-6y-10x+10y+32\)
\(=x^2-2.x\left(y+5\right)+\left(y+5\right)^2-\left(y+5\right)^2+4y^2+4y+32\)
\(=\left(x-y-5\right)^2-y^2-10y-25+4y^2+4y+32\)
\(=\left(x-y-5\right)^2+3y^2-6y+7\)
\(=\left(x-y-5\right)^2+3\left(y^2-2y+1\right)+4\)
\(=\left(x-y-5\right)^2+3\left(y-1\right)^2+4\)
Ta thấy : \(\left(x-y-5\right)^2+3\left(y-1\right)^2\ge0\forall x,y\)
\(\Rightarrow D\ge4\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x-y-5=0\\y-1=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x=6\\y=1\end{cases}}\)
Vậy : min \(D=4\) tại \(x=6,y=1\)

bài 1:= \(2x\left(x-3\right)-6\left(x-3\right)+2y\left(x-3\right)\)
=\(2\left(x-3\right)\left(x+y-3\right)\)
bài 2:P=\(x^2-2x+1+y^2+6y+9+2\)
P=\(\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\)
vậy Pmin=2 khi x=1 và y=-3

\(C=2\left(x^2-2x+1\right)+\left(y^2-6y+9\right)-19=2\left(x-1\right)^2+\left(y-3\right)^2-19\ge-19\)
\(minC=-19\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
bạn ơi sai đề bài à
4xy+2x^2+6y^2=32
2.(2xy+x^2+y^2)=32
(x+y)^2=32:2
(x+y)^2=16
(x+y)^2=8^2
x+y=8
<=>.....
đoạn dưới bn tự suy ra nhe. mik lười =>
4xy + 2x + 6y = 32
⇔ 4xy + 2x + 6y - 32 = 0
⇔ 2x( 2y + 1 ) + 3( 2y + 1 ) - 35 = 0
⇔ ( 2y + 1 )( 2x + 3 ) = 35
Ta có bảng sau :
Vậy ...