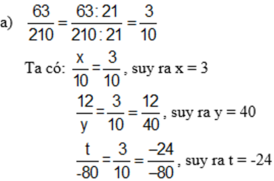K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 3 2017
Ta có : 2(x+y+z)=32\(\Rightarrow\) x+y+z=16
Mà x+y=5 \(\Rightarrow\) z=16-5=11
y+z=7 \(\Rightarrow\) y=7-11=-4
z+x=20\(\Rightarrow\) x=20-11=9
AH
Akai Haruma
Giáo viên
14 tháng 8 2023
Lời giải:
$7^x=50-12y=2(25-6y)\vdots 2$ (điều này vô lý với mọi $x$ là số tự nhiên)
Do đó không tồn tại $(x,y)$ thỏa mãn đề.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 8 2023
7\(x\) + 12y = 50
7\(^x\) là số lẻ với ∀ \(x\) \(\in\) N
12y là số chẵn với \(\forall\) y \(\in\) N
⇒ 7\(x\) + 12y là số lẻ khác với 50 là số chẵn
Vậy 7\(^x\) + 12y \(\ne\) 50 ∀ \(x;y\) \(\in\) N
Vậy (\(x;y\)) \(\in\) \(\varnothing\)
14 tháng 8 2023
Ta có : vậy { 0;1 }
và
với Không tìm được
với
Vậy x = 2 ; y = 0
❤ Nhớ k cho mk nha
# Chúc bạn học tốt❤
PT
1
8 tháng 4 2018
có nhiều trường hợp:
1. x=0; y=3;
2. x=2; y=2;
3. x=4; y=1
đấy là 1 số trg hợp nếu thiếu thì bổ sung nhé mn!
YN
15 tháng 4 2021
\(x^2-6y^2=1\)
\(\rightarrow y=2\Rightarrow x^2=4.6+1=25\Rightarrow x=5\)( thỏa mãn )
\(\rightarrow y>2\Rightarrow x>2\Rightarrow x;y\)lẻ \(\Rightarrow x^2;y^2\)chia \(4\) dư \(1\)\(\Rightarrow\)\(1\) chia \(4\)dư: \(1-2=-1\)( vô lý )
Vậy \(x=5;y=2\)