
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|x+3\right|+\left(y-x\right)^{10}+\left(z+x\right)^{20}=0\)
Ta có: \(\hept{\begin{cases}\left|x+3\right|\ge0\forall x\\\left(y-x\right)^{10}\ge0\forall x;y\\\left(z+x\right)^{20}\ge0\forall x;z\end{cases}}\)
Mà \(\left|x+3\right|+\left(y-x\right)^{10}+\left(z+x\right)^{20}=0\)
\(\Rightarrow\hept{\begin{cases}\left|x+3\right|=0\\\left(y-x\right)^{10}=0\\\left(z+x\right)^{20}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+3=0\\y-x=0\\z+x=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-3\\y=x\\z=-x\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-3\\y=-3\\z=3\end{cases}}}\)

- Đặt (x; y) = d nên x = d.m; y = d.n với (m;n) =1. Giả sử x ≤ y thì m ≤ n.
- Ta có: x.y = dm.dn= d2.mn
BCNN(x; y) = x y x ; y = d 2 m . n d = d . m . n
- Ta có: BCNN (x;y) = 10 và x. y = 20 nên d = x y B C N N ( x ; y ) = 20 10 = 2
=> 2.m.n =10 nên m.n = 5
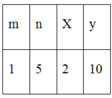
Bảng giá trị


\(ƯCLN\left(x;y\right)=\frac{xy}{BCNN\left(x;y\right)}=\frac{20}{10}=2\)
Đặt \(x=2k,y=2t\) (y và t là 2 số nguyên tố cùng nhau)
\(xy=20\Rightarrow2k.2t=20\Rightarrow k.t=5\)
\(\Rightarrow k\inƯ\left(5\right)=\left\{1;5\right\}\)
\(\Rightarrow x=2k\in\left\{2;10\right\}\)
Nếu x = 2 thì y = 10
Nếu x = 10 thì y = 2
Vậy x = 2 và y = 10 hoặc x = 10 và y = 2



Do trị tuyệt đối luôn lớn hơn hoặc = 0 nên
\(\left|x+20\right|=0;\left|y-11\right|=0;\left|x+200\right|=0\)
\(\Rightarrow x+20=0;y-11=0;z+200=0\)
\(\Rightarrow x=-20;y=11;z=-200\)
Chúc bn hok giỏi nha

a) 2y - 12y = 0
\(\Rightarrow\) y ( 2-12) = 0
\(\Rightarrow\) y . (-10) =0
\(\Rightarrow\) y = 0 : (-10) = 0
b) (y-7)(y-8) = 0
\(\Rightarrow\orbr{\begin{cases}y-7=0\\y-8=0\end{cases}\Rightarrow\orbr{\begin{cases}y=0+7\\y=0+8\end{cases}\Rightarrow}\orbr{\begin{cases}y=7\\y=8\end{cases}}}\)
c) x + x.2+x.3+x.4+...+x.10 = 165
\(\Rightarrow\) x ( 1+2+3+.....+8+9+10) = 165
\(\Rightarrow\)x . \(\frac{\left(1+10\right).10}{2}\)=165
\(\Rightarrow\) x . 55 = 165
\(\Rightarrow x=\frac{165}{55}=3\)
Can you k for me ,Lê Thị Kim Chi!
a) \(2y-12y=0\)
\(\Leftrightarrow-10y=0\)
\(\Leftrightarrow y=0:\left(-10\right)\)
\(\Leftrightarrow y=0\)
b) \(\left(y-7\right)\left(y-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y-7=0\\y-8=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}y=0+7\\y=0+8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}y=7\\y=8\end{cases}}\)
c) \(x+x.2+x.3+......+x.10=165\)
\(\Leftrightarrow x.\left(1+2+3+.....+10\right)=165\)
\(\Leftrightarrow x.55=165\)
\(\Leftrightarrow x=165:55\)
\(\Leftrightarrow x=3\)
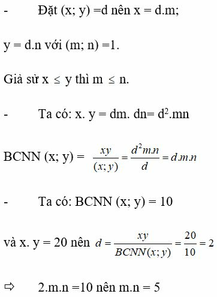

Ta có: \(\left(x-0,2\right)^{10}\ge0\) và \(\left(y+3,1\right)^{20}\ge0\) với mọi x, y
Tổng của 2 số dương = 0 khi và chỉ khi cả 2 số đó đều bằng 0.
=> \(\hept{\begin{cases}\left(x-0,2\right)^{10}=0\\\left(y+3,1\right)^{20}=0\end{cases}}\) => \(\hept{\begin{cases}x-0,2=0\\y+3,1=0\end{cases}}\)
=> \(\hept{\begin{cases}x=0,2\\y=-3,1\end{cases}}\)
ta thâý (x-0.2)10 > hoăc = 0 và (y+3.1)20 cũng > hoăc = 0 vì mũ chẵn. và (x-0.2)10 + (y+3.1)20 =0.
=> x-0.2 =0 => x=0.2
y+3.1=0 => y =-3.1