K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
2 tháng 2 2023
\(\dfrac{x}{8}=\dfrac{y}{12}\\ =>\dfrac{2x}{16}=\dfrac{3y}{36}\)
mà 2x+3y=12
áp dụng dãy tỉ số bằng nhau ta có
\(\dfrac{2x}{16}=\dfrac{3y}{36}=\dfrac{2x+3y}{16+36}=\dfrac{12}{52}=\dfrac{3}{13}\)
\(=>x=\dfrac{3}{13}\cdot8=\dfrac{24}{13}\\ y=\dfrac{3}{13}\cdot12=\dfrac{36}{13}\)
CM
4 tháng 5 2019
a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
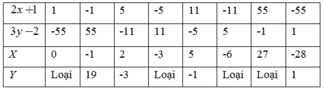
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
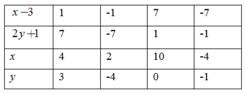
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.
EC
30 tháng 8 2016
Vì \(2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{12}{5}\)
\(\Rightarrow\begin{cases}\frac{x}{3}=\frac{12}{5}\\\frac{y}{2}=\frac{12}{5}\end{cases}\)\(\Rightarrow\begin{cases}x=\frac{36}{5}\\y=\frac{24}{5}\end{cases}\)
Vậy \(x=\frac{36}{5};y=\frac{24}{5}\)
30 tháng 8 2016
Ta có: \(2x=3y\Leftrightarrow x=\frac{3y}{2}\)
Ta lại có: \(x+y=12\)
Hay \(\frac{3y}{2}+y=12\)
\(\Leftrightarrow\frac{5y}{2}=12\)
\(\Leftrightarrow y=\frac{12\times2}{5}\)
\(\Leftrightarrow y=4.8\)
Vậy \(x=\frac{3y}{2}=7.2\)
TN
3
14 tháng 5 2016
\(2x\left(3y-2\right)+\left(3y-2\right)=-55\)
\(\left(3y-2\right)\left(2x+1\right)=-55\)
=> -55 chia hết cho 3y-2 và 2x+1 <=> 55chia hết cho 3y-2 và 2x+1
\(\Rightarrow3y-2\inƯ\left(55\right)\)và \(2x+1\inƯ\left(55\right)\)
Mà \(Ư\left(55\right)=\left\{-55;-11;-5;-1;1;5;11;55\right\}\)
Mặt khác 3y-2 chia 3 dư -2 (hay chia 3 dư1)
\(\Rightarrow3y-2\in\left\{-11;-5;1;55.\right\}\)
Ta có bảng sau
| 3y-2 | -11 | -5 | 1 | 55 |
| y | -3 | -1 | 1 | 19 |
| 2x+1 | 5 | 11 | -55 | -1 |
| x | 2 | 5 | -28 | 0 |
Vậy các cặp (x;y) cần tìm là :(2;-3),(5;-1),(-28;1),(0;19).
10 tháng 6 2021
Giải:
a) \(\left(x-4\right).\left(y+1\right)=8\)
\(\Rightarrow\left(x-4\right)\) và \(\left(y+1\right)\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
Ta có bảng giá trị:
| x-4 | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| y+1 | -1 | -2 | -4 | -8 | 8 | 4 | 2 | 1 |
| x | -4 | 0 | 2 | 3 | 5 | 6 | 8 | 12 |
| y | -2 | -3 | -5 | -9 | 7 | 3 | 1 | 0 |
Vì \(\left(x;y\right)\in N\) nên \(\left(x;y\right)=\left\{\left(5;7\right);\left(6;3\right);\left(8;1\right);\left(12;0\right)\right\}\)
Vậy \(\left(x;y\right)=\left\{\left(5;7\right);\left(6;3\right);\left(8;1\right);\left(12;0\right)\right\}\)
b) \(\left(2x+3\right).\left(y-2\right)=15\)
\(\Rightarrow\left(2x+3\right)\) và \(\left(y-2\right)\inƯ\left(15\right)=\left\{\pm1;\pm3;\pm5;\pm15\right\}\)
| 2x+3 | -15 | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| y-2 | -1 | -3 | -5 | -15 | 15 | 5 | 3 | 1 |
| x | -9 | -4 | -3 | -2 | -1 | 0 | 1 | 6 |
| y | 1 | -1 | -3 | -13 | 17 | 7 | 5 | 3 |
Vì \(\left(x;y\right)\in N\) nên \(\left(x;y\right)\in\left\{\left(0;7\right);\left(1;5\right);\left(6;3\right)\right\}\)
Vậy \(\left(x;y\right)\in\left\{\left(0;7\right);\left(1;5\right);\left(6;3\right)\right\}\)
c) \(xy+2x+y=12\)
\(\Rightarrow x.\left(y+2\right)+\left(y+2\right)=14\)
\(\Rightarrow\left(x+1\right).\left(y+2\right)=14\)
\(\Rightarrow\left(x+1\right)\) và \(\left(y+2\right)\inƯ\left(14\right)=\left\{1;2;7;14\right\}\)
| x+1 | 1 | 2 | 7 | 14 |
| y+2 | 14 | 7 | 2 | 1 |
| x | 0 | 1 | 6 | 13 |
| y | 12 | 5 | 0 | -1 |
Vì \(\left(x;y\right)\in N\) nên \(\left(x;y\right)\in\left\{\left(0;12\right);\left(1;5\right);\left(6;0\right)\right\}\)
Vậy \(\left(x;y\right)\in\left\{\left(0;12\right);\left(1;5\right);\left(6;0\right)\right\}\)
d) \(xy-x-3y=4\)
\(\Rightarrow y.\left(x-3\right)-\left(x-3\right)=7\)
\(\Rightarrow\left(y-1\right).\left(x-3\right)=7\)
\(\Rightarrow\left(y-1\right)\) và \(\left(x-3\right)\inƯ\left(7\right)=\left\{1;7\right\}\)
Ta có bảng giá trị:
| x-3 | 1 | 7 |
| y-1 | 7 | 1 |
| x | 4 | 10 |
| y | 8 | 2 |
Vậy \(\left(x;y\right)\in\left\{\left(4;8\right);\left(10;2\right)\right\}\)
15 tháng 12 2016
ta thấy 12 = 1 x 12 = 3 x 4 = 2 x 6
vậy ta xét 6 TH
TH1 2x+1=1=> x=0
và 3y- 2= 12=> y= 14/3
.......
các TH còn lại bn tự xét nhé
KS
1
21 tháng 12 2015
\(\frac{4}{x}=\frac{7}{y}=\frac{12}{z}=>\frac{8}{2x}=\frac{21}{3y}=\frac{48}{4z}=\frac{8+21+48}{1925}=\frac{77}{1925}=\frac{1}{25}\)
=>4/x=1/25=>x=100
=>7/y=1/25=>y=175
=>12/z=1/25=>z=300
a)Ta có 18=2.32
Mà theo đề ra ta có 18=2x.3y
=>x=1 và y=2
b)Ta có 12=22.3
Mà theo đề ra ta có 12=2x.3y
=>x=2 và y=1