Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có tg QPNM có góc Q+ góc P + góc N+ góc M=360 độ
Suy ra 4x + 3x +2x +x =360 độ
suy ra. 10x =360 độ
suy ra. X= 36 độ
Hình số 2
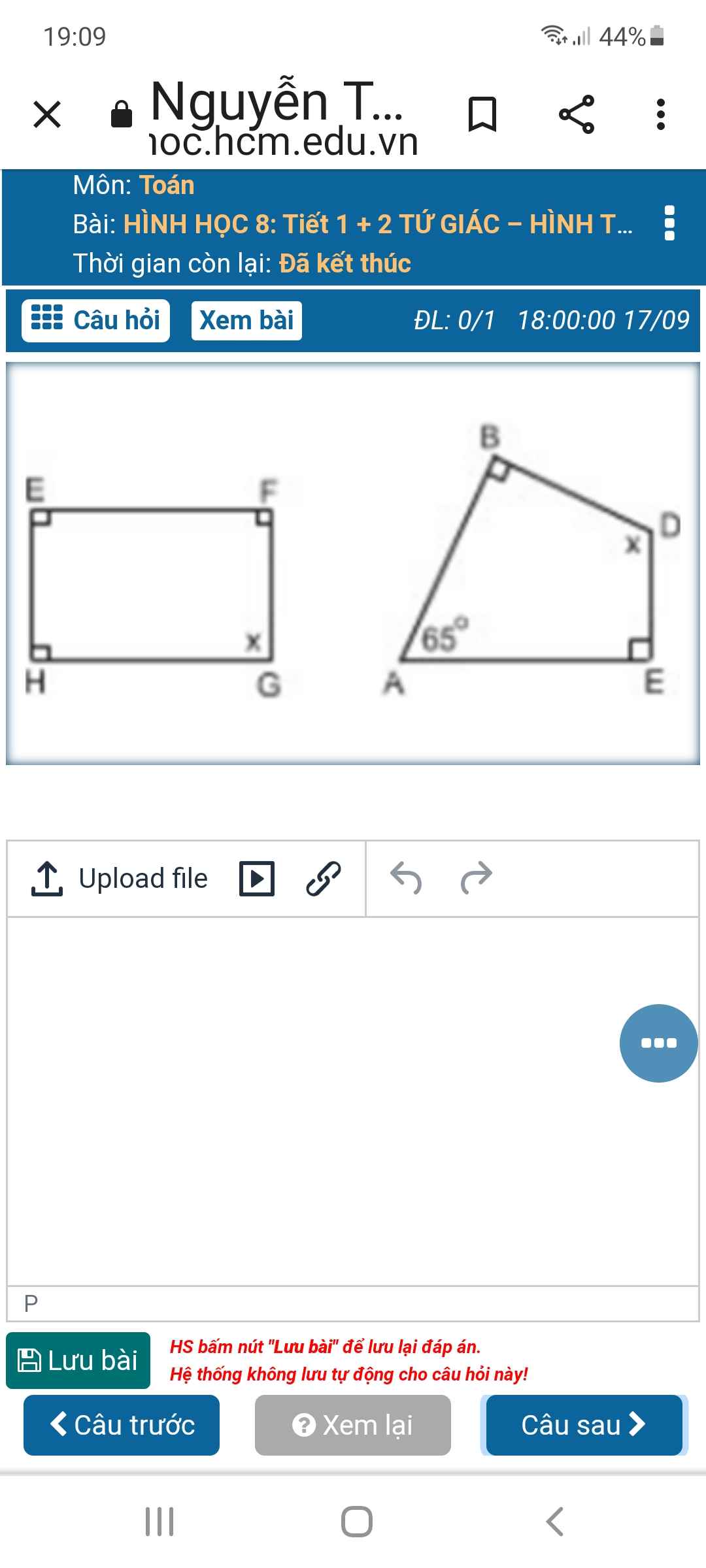
Ta có tg ABCD có góc A+ góc B + góc C+ góc D =360 độ
Suy ra. X+2x+2x+x=360 độ
suy ra. 6x=360 độ
suy ra. X. =60 độ
hình QPMN:
x + 2x + 3x + 4x = 360o
⇒ 10x = 360o
⇒ x = 36o Vậy x=36o
hình ABCD:
x+x+2x+2x=360o
⇒ 6x=360o
⇒ x=60o vậy x=60o

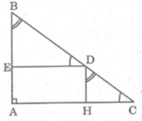
* ∠ B = ∠ (HDC)
⇒ AB // DH (vì có cặp góc đồng vị bằng nhau)
Hay DH //AE
* ∠ C = ∠ (BDE)
⇒ DE // AC (vì có cặp góc đồng vị bằng nhau)
Hay DE //AH
Vậy tứ giác AHDE là hình bình hành ( có các cặp đối song song với nhau )
Mà ∠ A = 90 0 nên AHDE là hình chữ nhật

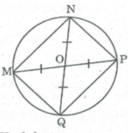
Tứ giác MNPQ có:
OM = OP = R nên O là trung điểm của MP
ON = OQ = R nên O là trung điểm của NQ
Tứ giác MNPQ có O là trung điểm của mỗi đường chéo
Suy ra:Tứ giác MNPQ là hình bình hành
Lại có: MP = NQ = 2R ( = đường kính của đường tròn)
Nên tứ giác MNPQ là hình chữ nhật

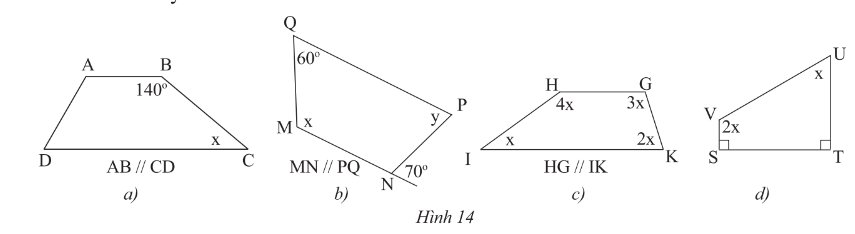
a) Vì \(AB\) // \(CD\) (gt) suy ra:
\(\widehat B + \widehat C = 180^\circ \) (cặp góc trong cùng phía)
\(\begin{array}{l}140^\circ + x = 180^\circ \\x = 40^\circ \end{array}\)
b) Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat M + \widehat Q = 180^\circ \) (trong cùng phía)
\(\begin{array}{l}x + 60^\circ = 180^\circ \\x = 120^\circ \end{array}\)
Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat P = \widehat N = 70^\circ \) (so le trong)
c) Xét tứ giác \(IHGK\) ta có:
\(\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}\)
d) Xét tứ giác \(UVST\) ta có:
\(\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ \)
\(\begin{array}{l}x + 2x + 90^\circ + 90^\circ = 360^\circ \\3x + 180^\circ = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}\)

vì AD là phân giác góc A của tam giác BAC
=>\(\dfrac{AB}{AC}=\dfrac{BD}{DC}< =>\dfrac{x}{5}=\dfrac{5,1}{3}=>x=\dfrac{5.5,1}{3}=8,5cm\)