K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
17 tháng 2 2018
\(\left(-3-x\right)\left(x+5\right)=0\)
\(\Rightarrow\orbr{\begin{cases}-3-x=0\\x+5=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-3\\x=-5\end{cases}}\)
IA
9 tháng 6 2018
Bài 1 :
\(3x+5=2\left(x-\frac{1}{4}\right)\)
\(\Leftrightarrow3x+5=2x-\frac{1}{2}\)
\(\Leftrightarrow5+\frac{1}{2}=2x-3x\)
\(\Leftrightarrow\frac{11}{2}=-x\)
\(\Leftrightarrow\frac{-11}{2}=x\)
Vậy \(x=\frac{-11}{2}\)
Bài 2:
a, \(\left|x+\frac{19}{5}\right|+\left|y+\frac{2018}{2019}\right|+\left|z-3\right|=0\)
Vì \(\hept{\begin{cases}\left|x+\frac{19}{5}\right|\ge0\\\left|y+\frac{2018}{2019}\right|\ge0\\\left|z-3\right|\ge0\end{cases}}\)
Mà \(\left|x+\frac{19}{5}\right|+\left|y+\frac{2018}{2019}\right|+\left|z-3\right|=0\)
\(\Rightarrow+,\left|x+\frac{19}{5}\right|=0\)
\(\Leftrightarrow x+\frac{19}{5}=0\)
\(\Leftrightarrow x=\frac{-19}{5}\)
\(\Rightarrow+,\left|y+\frac{2018}{2019}\right|=0\)
\(\Leftrightarrow y+\frac{2018}{2019}=0\)
\(\Leftrightarrow y=\frac{-2018}{2019}\)
\(\Rightarrow+,\left|z-3\right|=0\)
\(\Leftrightarrow z-3=0\)
\(\Leftrightarrow z=3\)
Vậy \(\hept{\begin{cases}x=\frac{-19}{5}\\y=\frac{-2018}{2019}\\z=3\end{cases}}\)
b, Ta có : \(\left|x-\frac{1}{2}\right|+\left|2y+4\right|+\left|z-5\right|\ge0\)
Vì : \(\hept{\begin{cases}\left|x-\frac{1}{2}\right|\ge0\\\left|2y+4\right|\ge0\\\left|z-5\right|\ge0\end{cases}}\)
Mà : \(\left|x-\frac{1}{2}\right|+\left|2y+4\right|+\left|z-5\right|\ge0\)
\(\Rightarrow+,\left|x-\frac{1}{2}\right|\ge0\)
\(\Rightarrow x\inℚ\)
\(\Rightarrow+,\left|2y+4\right|\ge0\)
\(\Rightarrow y\inℚ\)
\(\Rightarrow+,\left|z-5\right|\ge0\)
\(\Rightarrow z\inℚ\)
Vậy chỉ cần \(\hept{\begin{cases}x\inℚ\\y\inℚ\\z\inℚ\end{cases}}\)thì thỏa mãn.
VQ
0
TN
2
9 tháng 2 2017
(x - 5)x+1 - (x - 5)x+9 = 0
(x - 5)x+1 - (x - 5)x+1.(x - 5)8 = 0
(x - 5 )x+1[1 - (x - 5)8] = 0
\(\Rightarrow\orbr{\begin{cases}\left(x-5\right)^{x+1}=0\\1-\left(x-5\right)^8=0\end{cases}\Rightarrow\orbr{\begin{cases}x-5=0\\\left(x-5\right)^8=1\end{cases}\Rightarrow}\orbr{\begin{cases}x=5\\x=4;6\end{cases}}}\)
Vậy x = { 4;5;6 }
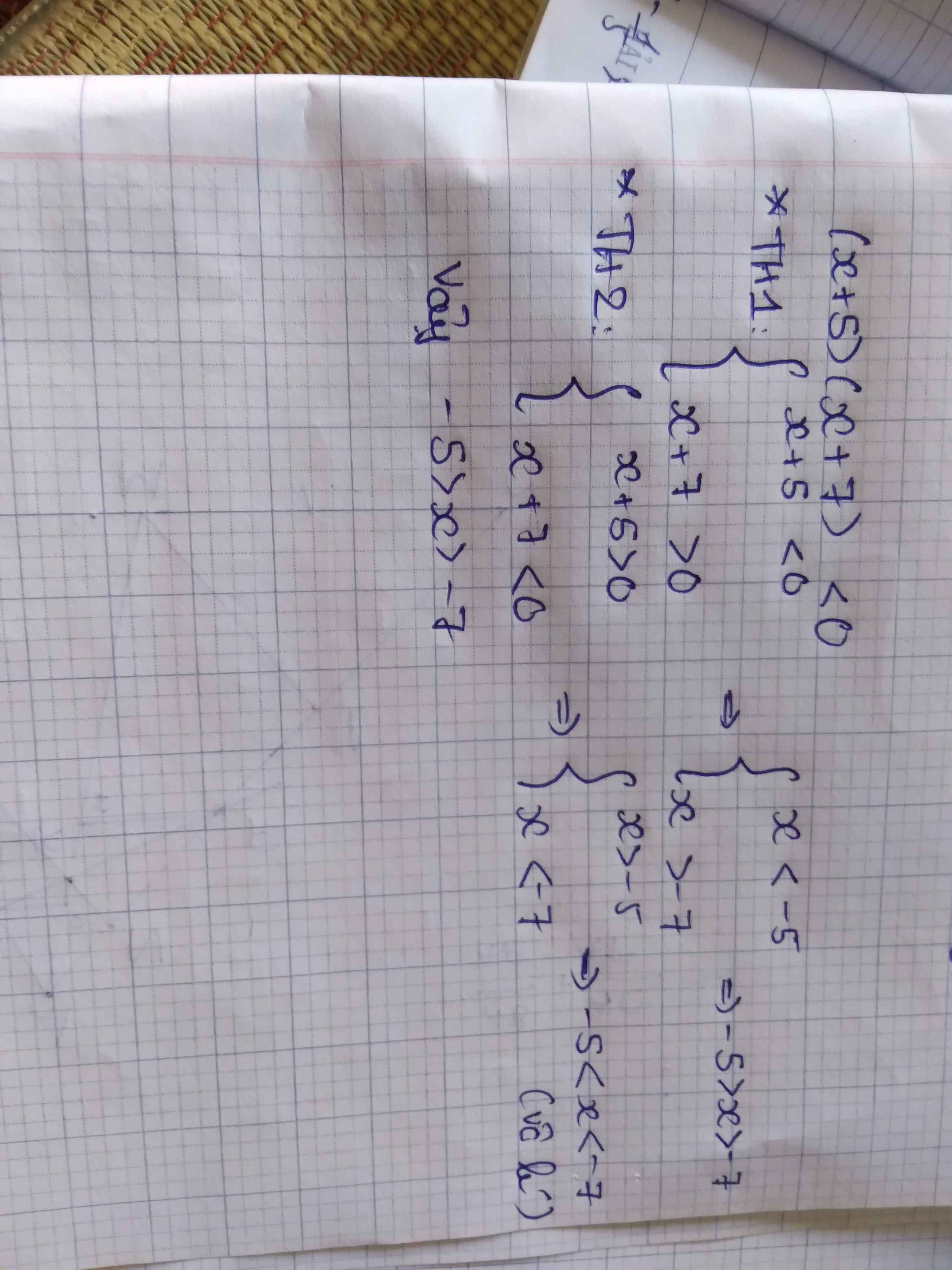
=> x-1<0 hoăc 5-x<0
<=> x < 1 x < -5
Vây x < 1 hoac x < -5
\(\left(x-1\right)\left(5-x\right)< 0\)
TH1: \(\hept{\begin{cases}x-1< 0\\5-x>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 1\\5>x\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 1\\x< 5\end{cases}}\Leftrightarrow x< 1\)
TH2: \(\hept{\begin{cases}x-1>0\\5-x< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>1\\5< x\end{cases}}\Leftrightarrow\hept{\begin{cases}x>1\\x>5\end{cases}}\Leftrightarrow x>5\)
Vậy \(x< 1\)hoặc \(x>5\)