Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{x+2}{x+1}=1+\dfrac{1}{x+1}\)
Để A nguyên :
\(x+1\inƯ\left(1\right)\\ Ư\left(1\right)=\left\{1;-1\right\}\\ \Rightarrow\left\{{}\begin{matrix}x+1=1\\x+1=-1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)



a: \(-\dfrac{15}{20};\dfrac{24}{-32};-\dfrac{27}{36}\)


a) \(F=\frac{3x-2}{x+3}\)là số nguyên
\(\Leftrightarrow3x-2⋮x+3\)
\(\Leftrightarrow3x+9-11⋮x+3\)
\(\Leftrightarrow3\left(x+3\right)-11⋮x+3\)
\(\Leftrightarrow11⋮x+3\)\(\Leftrightarrow x+3\in\left\{-11;-1;1;11\right\}\)
\(\Leftrightarrow x\in\left\{-14;-4;-2;8\right\}\)
b) \(\frac{x^2-2x+4}{x+1}\)là số nguyên
\(\Leftrightarrow x^2-2x+4⋮x+1\)
\(\Leftrightarrow x^2+x-3x-3+7⋮x+1\)
\(\Leftrightarrow x\left(x+1\right)-3\left(x+1\right)+7⋮x+1\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)+7⋮x+1\)
\(\Leftrightarrow7⋮x+1\)\(\Leftrightarrow x+1\in\left\{-7;-1;1;7\right\}\)
\(\Leftrightarrow x\in\left\{-8;-2;0;6\right\}\)

Bạn An phát biểu sai vì 0 là số hữu tỉ(vì \(0=\dfrac{0}{1}\))
Bạn Bình phát biểu sai vì phải thêm điều kiện \(b\ne0\) nữa thì \(\dfrac{a}{b}\) mới là số hữu tỉ
Bạn Chi nói đúng vì tất cả các số nguyên a đều viết được dưới dạng \(\dfrac{a}{1}\) nên chúng là số hữu tỉ
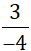 ?
?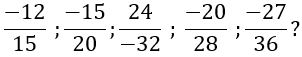
A là số nguyên `<=> -2 vdots (x+1)`
`<=> x+1 \in {-2;2;-1;1}`
`<=> x \in {-3;1;-2;0}
B là số nguyên `<=>2x+5 vdots x+1`
`<=> (2x+2)+3 vdots x+1`
`<=> 3 vdots x+1`
`<=> x+1 \in {-3;3;-1;1}`
`<=> x \in {-4;2;-2;0}`
em cảm ơn ạ