DM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CB
0
M
1
18 tháng 3 2016
Gọi \(A=\frac{1005}{2011}\)
A=1/3 + 1/3.5 + 1/5.7 +...............+1/x.(x+2)
A=1/1.3 + 1/3.5 + 1/5.7 +...............+1/x.(x+2)
A . 2=2/1.3 + 2/3.5 + 2/5.7 +......................+2/x.(x+2)
A . 2=1/1-1/3+1/3-1/5+1/5-1/7+..............+1/x-1/x+2
A . 2=1/1+(1/3-1/3)+(1/5-1/5)+..............+(1/x-1/x)-1/x+2
A . 2=1/1-1/x+2
Suy gia:1005/2011 . 2=1/1-1/x+2
2010/2011 =1/1-1/x+2
1/x+2 =1/1-2010/2011
1/x+2 =1/2011
Suy gia:x+2=2011
x =2011-2
x =2009
H
15 tháng 5 2017
Có:
\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{x.\left(x+2\right)}=\dfrac{5}{11}\)
\(\Rightarrow\dfrac{1}{2}.\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{x}-\dfrac{1}{x+2}\right)=\dfrac{5}{11}\)
\(\Rightarrow\dfrac{1}{2}.\left(1-0-0-0...-0-\dfrac{1}{x+2}\right)=\dfrac{5}{11}\)
\(\Rightarrow\dfrac{1}{2}.\left(1-\dfrac{1}{x+2}\right)=\dfrac{5}{11}\)
\(\Rightarrow1-\dfrac{1}{x+2}=\dfrac{5}{11}:\dfrac{1}{2}=\dfrac{10}{11}\)
\(\Rightarrow\dfrac{1}{x+2}=1-\dfrac{10}{11}\)
\(\Rightarrow\dfrac{1}{x+2}=\dfrac{1}{11}\)
\(\Rightarrow x+2=11\)
\(\Rightarrow x=11-2=9\)
Vậy x = 9.
Chúc bạn học tốt!
15 tháng 5 2017
1/1.3 + 1/3.5 + 1/5.7 + ... +1/x.(x+2)
= 1/2.(1/1 - 1/3) + 1/2.(1/3 - 1/5) + 1/2.(1/5 - 1/7) + ... + 1/2.(1/x -1/x+2)
= 1/2.(1/1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ... + 1/x - 1/x+2 )
= 1/2.(1/1 - 0 - 1/x+2 )
= 1/2 . ( 1/1 - 1/x+2 )
= 1/2 . ( x+2/x+2 - 1/x+2 )
= 1/2 . x+1/x+2
Mà 1/1.3 + 1/3.5 + 1/5.7 + ... +1/x.(x+2) = 5/11
=> 1/2 . x+1/x+2 = 5/11
=> x+1/x+2 = 5/11 : 1/2
=> x+1/x+2 = 10/11
=> x+1/x+2-1 = 10/11-1
=> x+1/x+1 = 10/10
=> x + 1 = 10
=> x = 10 - 1
=> x = 9
Vậy x = 9
SC
3
26 tháng 4 2015
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{x\left(x+2\right)}=\frac{20}{41}\)
\(\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{x\left(x+2\right)}\right)=\frac{20}{41}\)
\(\frac{1}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}\right)=\frac{20}{41}\)
\(\frac{1}{2}\left(1-\frac{1}{x+2}\right)=\frac{20}{41}\)
\(\frac{1}{2}.\frac{x+1}{x+2}=\frac{20}{41}\)
\(\frac{x+1}{x+2}=\frac{20}{41}:\frac{1}{2}\)
\(\frac{x+1}{x+2}=\frac{40}{41}\)
\(x+1=40
\)
\(x=40-1\)
\(x=39\)
Đúng thì ****
NH
2
C
6 tháng 5 2022
\(P=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2021.2023}\)
\(2P=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{3}{5.7}+...+\dfrac{2}{2021.2023}\)
\(2P=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(2P=\dfrac{1}{1}-\dfrac{1}{2023}\)
\(P=\dfrac{2022}{2023}:2\)
\(P=\dfrac{1011}{2023}\)
TC
6 tháng 5 2022
\(=>P=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(P=1-\dfrac{1}{2023}=\dfrac{2023}{2023}-\dfrac{1}{2023}=\dfrac{2022}{2023}\)
\(x.P=\dfrac{2022}{2023}=>x=P:\dfrac{2022}{2023}=\dfrac{2022}{2023}:\dfrac{2022}{2023}=1\)
21 tháng 8 2021
Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{x\left(x+2\right)}=\dfrac{20}{41}\)
\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{40}{41}\)
\(\Leftrightarrow1-\dfrac{2}{x+2}=\dfrac{40}{41}\)
\(\Leftrightarrow\dfrac{2}{x+2}=\dfrac{1}{41}\)
Suy ra: x+2=82
hay x=80
DP
2 tháng 8 2017
Sửa đề . \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{n\left(n+2\right)}=\frac{71}{216}\)
\(\Leftrightarrow\frac{1}{2}.\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{n}-\frac{1}{n+2}\right)=\frac{71}{216}\)
\(\Leftrightarrow\frac{1}{2}.\left(1-\frac{1}{n+2}\right)=\frac{71}{216}\)
\(\Leftrightarrow\frac{1}{n+2}=1-\frac{71}{216}\div\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{n+2}=\frac{37}{108}\)
\(\Leftrightarrow x=\frac{34}{37}\Rightarrow\text{(đề sai) }\)
NN
2
BI
25 tháng 3 2016
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{x.\left(x+2\right)}=\frac{5}{11}\)
\(\Rightarrow\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}\right)=\frac{5}{11}\)
\(\Rightarrow\frac{1}{2}\left(1-\frac{1}{x+2}\right)=\frac{5}{11}\Rightarrow1-\frac{1}{x+2}=\frac{5}{11}\div\frac{1}{2}=\frac{10}{11}\)
\(\Rightarrow\frac{1}{x+2}=1-\frac{10}{11}=\frac{1}{11}\Rightarrow x+2=11\Rightarrow x=11-2=9\)
25 tháng 3 2016
\(\frac{1}{1.3}+\frac{1}{3.5}+......+\frac{1}{x+\left(x+2\right)}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+........+\frac{1}{x}-\frac{1}{x+2}\)
\(=1-\frac{1}{x+2}=\frac{5}{11}\)
\(\frac{1}{x+2}=1-\frac{5}{11}=\frac{6}{11}\)
=> không có kết quả
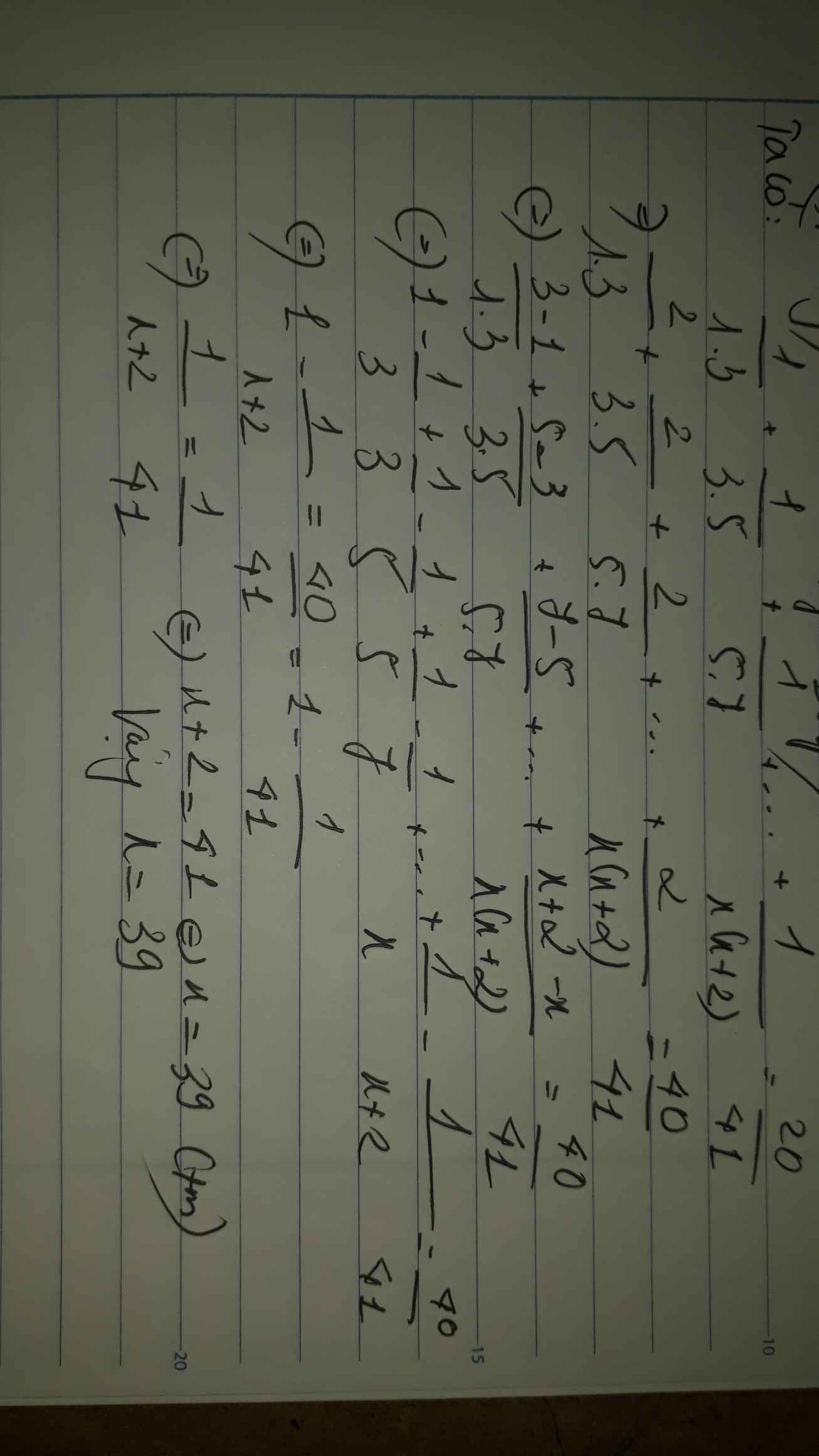
\(\Leftrightarrow\frac{1}{2}\left(\frac{2}{1\cdot3}+\frac{2}{3\cdot5}+...+\frac{2}{\left(5x+1\right)\left(5x+3\right)}\right)=\frac{11}{23}\)
\(\Leftrightarrow\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{5x+1}-\frac{1}{5x+3}\right)=\frac{11}{23}\)
\(\Leftrightarrow1-\frac{1}{5x+3}=\frac{22}{23}\)
\(\Leftrightarrow\frac{1}{5x+3}=\frac{1}{23}\)
\(\Leftrightarrow5x+3=23\Leftrightarrow x=4\) ( TM )
\(\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{\left(5x+1\right).\left(5x+3\right)}=\frac{11}{23}\)
\(\Rightarrow\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{\left(5x+1\right)\left(5x+3\right)}\right)=\frac{11}{23}\)
\(\Rightarrow\frac{1}{2}\left(1-\frac{1}{3}+...+\frac{1}{\left(5x+1\right)}-\frac{1}{\left(5x+3\right)}\right)=\frac{11}{23}\)
\(\Rightarrow1-\frac{1}{\left(5x+3\right)}=\frac{11}{23}:\frac{1}{2}\)
\(\Rightarrow\frac{1}{5x+3}=\frac{1}{23}\)
\(\Rightarrow5x+3=23\)
\(\Rightarrow5x=23-3\)
\(\Rightarrow x=20:5\)
\(\Rightarrow x=4\)