
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-3\right)=\left(3-x\right)^2\)
\(\Leftrightarrow x-3=\left(x-3\right)^2\)
\(\Leftrightarrow\left(x-3\right)-\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x-3\right)\left[1-\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\4-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
___________
\(x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}=\dfrac{1}{64}\)
\(\Leftrightarrow x^3+3\cdot\dfrac{1}{2}\cdot x^2+3\cdot\left(\dfrac{1}{2}\right)^2\cdot x+\left(\dfrac{1}{2}\right)^3=\dfrac{1}{64}\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^3=\left(\dfrac{1}{4}\right)^3\)
\(\Leftrightarrow x+\dfrac{1}{2}=\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{1}{4}-\dfrac{1}{2}\)
\(\Leftrightarrow x=-\dfrac{1}{4}\)

a: TH1: x>=3 hoặc x<=0
=>x^2-3x=5x
=>x^2-8x=0
=>x=0(nhận) hoặc x=8(nhận)
TH2: 0<x<3
=>3x-x^2=5x
=>-x^2-2x=0
=>x=0(loại) hoặc x=-2(loại)
b: TH1: x>=0 hoặc x<=-5
=>x^2+5x=6x
=>x^2-x=0
=>x=0(nhận) hoặc x=1(nhận)
TH2: -5<x<0
=>-x^2-5x=6x
=>-x^2-11x=0
=>x=0(loại) hoặc x=-11(loại)
c: TH1: x>=0 hoặc x<=-2
=>x^2+2x=-x
=>x^2+3x=0
=>x=0(nhận) hoặc x=-3(nhận)
TH2: -2<x<0
=>-x^2-2x=x
=>x^2+2x=x
=>x^2+x=0
=>x=0(loại) hoặc x=-1(nhận)
c: TH1: x>=1 hoặc x<=0
=>x^2-x=x-1
=>x^2-2x+1=0
=>x=1(nhận)
TH2: 0<x<1
=>-x^2+x=x-1
=>-x^2=-1
=>x=1(loại) hoặc x=-1(loại)

\(x^3-3x^2+3x-1=-8\)
\(\Leftrightarrow x-1=-2\)
hay x=-1

\(a,=xy\left(5x-1\right)\\ b,=\left(x-2\right)\left(3x-5\right)\\ c,Sửa:x^2+2x+1-9y^2\\ =\left(x+1\right)^2-9y^2\\ =\left(x-3y+1\right)\left(x+3y+1\right)\\ d,=x\left(x-y\right)+5\left(x-y\right)=\left(x+5\right)\left(x-y\right)\)



Ta có: \(x+y+z=0\)
nên \(\left\{{}\begin{matrix}x+y=-z\\x+z=-y\\y+z=-x\end{matrix}\right.\)
Ta có: \(P=\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)\)
\(=\dfrac{x+y}{y}\cdot\dfrac{y+z}{z}\cdot\dfrac{x+z}{x}\)
\(=\dfrac{-z}{y}\cdot\dfrac{-x}{z}\cdot\dfrac{-y}{x}\)
\(=\dfrac{-\left(x\cdot y\cdot z\right)}{x\cdot y\cdot z}=-1\)

a) Ta có: \(A=x\left(x+2\right)+y\left(y-2\right)-2xy+37\)
\(=x^2+2x+y^2-2y-2xy+37\)
\(=\left(x^2-2xy+y^2\right)+\left(2x-2y\right)+37\)
\(=\left(x-y\right)^2+2\left(x-y\right)+37\)
\(=\left(x-y\right)\left(x-y+2\right)+37\)(1)
Thay x-y=7 vào biểu thức (1), ta được:
\(A=7\cdot\left(7+2\right)+37=7\cdot9+37=100\)
Vậy: Khi x-y=7 thì A=100
b) Ta có: \(x+y=2\)
\(\Leftrightarrow\left(x+y\right)^2=4\)
\(\Leftrightarrow x^2+y^2+2xy=4\)
\(\Leftrightarrow2xy+10=4\)
\(\Leftrightarrow2xy=-6\)
\(\Leftrightarrow xy=-3\)
Ta có: \(A=x^3+y^3\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)\)(2)
Thay x+y=2; \(x^2+y^2=10\) và xy=-3 vào biểu thức (2), ta được:
\(A=2\cdot\left(10+3\right)=2\cdot13=26\)
Vậy: Khi x+y=2 và \(x^2+y^2=10\) thì A=26
\(\Rightarrow A=x^2+2x+y^2-2y-2xy+37=x^2-2xy+y^2+2\left(x-y\right)+37=\left(x-y\right)^2+2\left(x-y\right)+37=7^2+2\cdot7+37=100\)
\(\Rightarrow A=x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)=\left(x+y\right)\left[x^2+y^2-\dfrac{\left(x+y\right)^2-\left(x^2+y^2\right)}{2}\right]=2\cdot\left[10+3\right]=2\cdot13=26\) \(\Rightarrow\left\{{}\begin{matrix}x+y=-z\\x+z=-y\\y+z=-x\end{matrix}\right.\) \(\Rightarrow P=\left(\dfrac{x+y}{y}\right)\left(\dfrac{y+z}{z}\right)\left(\dfrac{x+z}{x}\right)=-\dfrac{z}{y}\cdot\dfrac{-x}{z}\cdot-\dfrac{y}{x}=-1\)

\(1,\)
\(2x\left(x-3\right)-\left(3-x\right)=0\)
\(\Leftrightarrow2x\left(x-3\right)+\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=3\end{cases}}\)
\(2,\)
\(3x\left(x+5\right)-6\left(x+5\right)=0\)
\(\Leftrightarrow\left(3x-6\right)\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x-6=0\\x+5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-5\end{cases}}\)
\(3,\)
\(x^4-x^2=0\)
\(\Leftrightarrow x^2\left(x^2-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=0\\x^2-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm1\end{cases}}\)
\(4,\)
\(x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
\(5,\)
\(x\left(x+6\right)-10\left(x-6\right)=0\)
\(\Leftrightarrow x^2+6x-10x+60=0\)
\(\Leftrightarrow x^2-4x+60=0\)
\(\Leftrightarrow x^2-4x+4+56=0\)
\(\Leftrightarrow\left(x-2\right)^2=-56\)(Vô lý)
=> Phương trình vô nghiệm

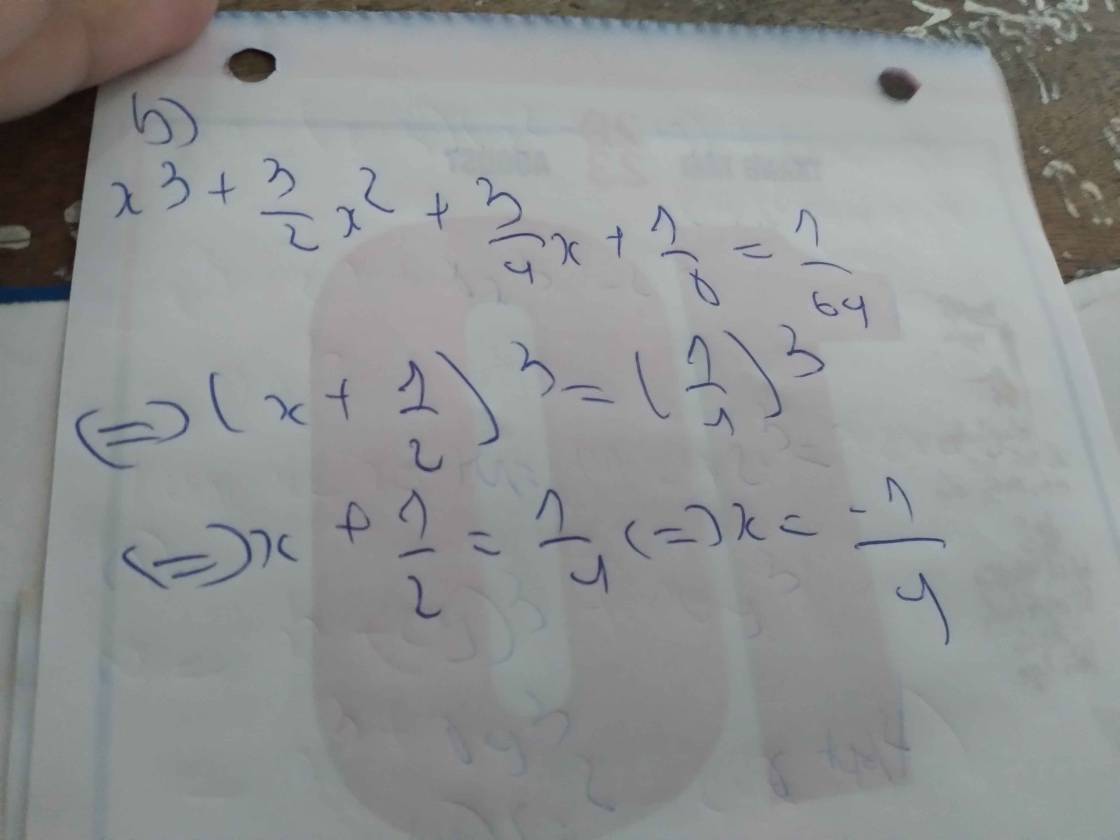
x(x+1) (x+6)-x3=5x
<=> ( x2 + x ) . ( x + 6 ) - x3 - 5x = 0
<=> x3 +6x2 +x2 + 6x - x3 -5x = 0
<=> 7x2 + x = 0
<=> x ( 7x + 1 ) = 0
<=> \(\orbr{\begin{cases}x=0\\7x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=0\\x=-\frac{1}{7}\end{cases}}\)
Vay : phương trình có 2 nghiệm \(x_1=0;x_2=-\frac{1}{7}\)
CHÚC BẠN HỌC TỐT !!!
\(x\left(x+1\right)\left(x+6\right)-x^3=5x\)
\(< =>x^3+7x^2+6x-x^3-5x=0\)
\(< =>7x^2+x=0\)
\(< =>x\left(7x+1\right)=0\)
\(< =>\orbr{\begin{cases}x=0\\7x+1=0\end{cases}}\)
\(< =>\orbr{\begin{cases}x=0\\x=-\frac{1}{7}\end{cases}}\)