DT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 9 2020
Bài chỉ chứng minh vế phải chia hết vế trái chứ k tìm n hay a nhé bạn
AH
Akai Haruma
Giáo viên
11 tháng 9 2020
Nguyễn Ngọc Phương: Mình đâu có tìm $n,a$ đâu hả bạn? Mình đang chỉ ra TH sai mà???
Chả hạn, chứng minh $n(n+1)(n^2+1)\vdots 5$ thì có nghĩa mọi số tự nhiên/ nguyên $n$ đều phải thỏa mãn. Nhưng chỉ cần có 1 TH $n$ thay vào không đúng nghĩa là đề không đúng rồi.
12 tháng 6 2023
a: \(=4\sqrt[3]{2}-9\sqrt[3]{2}++6\sqrt[3]{2}=\sqrt[3]{2}\)
b: \(=6\sqrt[3]{3}-15\sqrt[3]{3}+16\sqrt[3]{3}=7\sqrt[3]{3}\)
c: \(=-7\sqrt[3]{3}+3\sqrt[3]{3}+6\sqrt[3]{3}=2\sqrt[3]{3}\)
d: \(=8\sqrt[3]{5}-10\sqrt[3]{5}+2=-2\sqrt[3]{5}+2\)
AT
29 tháng 7 2021
câu đầu có \(3-12\sqrt{6}< 0\) nên không căn được nên đề bạn sai
\(\sqrt{31-8\sqrt{15}}+\sqrt{24-6\sqrt{15}}\)
\(=\sqrt{4^2-2.4.\sqrt{15}+\left(\sqrt{15}\right)^2}+\sqrt{\left(\sqrt{15}\right)^2-2.\sqrt{15}.3+3^2}\)
\(=\sqrt{\left(4-\sqrt{15}\right)^2}+\sqrt{\left(\sqrt{15}-3\right)^2}=\left|4-\sqrt{15}\right|+\left|\sqrt{15}-3\right|\)
\(=4-\sqrt{15}+\sqrt{15}-3=1\)
\(\sqrt{49-5\sqrt{96}}-\sqrt{49+5\sqrt{96}}=\sqrt{49-20\sqrt{6}}-\sqrt{49+20\sqrt{6}}\)
\(=\sqrt{5^2-2.5.2\sqrt{6}+\left(2\sqrt{6}\right)^2}-\sqrt{5^2+2.5.4\sqrt{6}+\left(2\sqrt{6}\right)^2}\)
\(=\sqrt{\left(5-2\sqrt{6}\right)^2}-\sqrt{\left(5+2\sqrt{6}\right)^2}=\left|5-2\sqrt{6}\right|-\left|5+2\sqrt{6}\right|\)
\(=5-2\sqrt{6}-5-2\sqrt{6}=-4\sqrt{6}\)
29 tháng 7 2021
\(\sqrt{31-8\sqrt{15}}+\sqrt{24-6\sqrt{15}}\)
\(=4-\sqrt{15}+\sqrt{15}-3\)
=1
KH
22 tháng 8 2019
\(a.\\ \left(\sqrt{4.3}-\sqrt{16.3}-\sqrt{36.3}-\sqrt{64.3}\right)\\ =\left(2\sqrt{3}-4\sqrt{3}-6\sqrt{3}-8\sqrt{3}\right):2\sqrt{3}\\ =\frac{-16\sqrt{3}}{2\sqrt{3}}=-8\)
\(b.\\ =\left(2\sqrt{16.7}-5\sqrt{7}+2\sqrt{9.7}-2\sqrt{4.7}\right)\sqrt{7}\\ =\left(8\sqrt{7}-5\sqrt{7}+6\sqrt{7}-4\sqrt{7}\right)\sqrt{7}\\ =5\sqrt{7}.\sqrt{7}=5.7=35\)
\(c.\\ =\left(2\sqrt{9.3}-3\sqrt{16.3}+3\sqrt{25.3}-\sqrt{64.3}\right)\left(1-\sqrt{3}\right)\\ =\left(6\sqrt{3}-12\sqrt{3}+15\sqrt{3}-8\sqrt{3}\right)\left(1-\sqrt{3}\right)\\ =\sqrt{3}\left(1-\sqrt{3}\right)\\ =\sqrt{3}-3\)
\(d.\\ =7\sqrt{4.6}-\sqrt{25.6}-5\sqrt{9.6}\\ =14\sqrt{6}-5\sqrt{6}-15\sqrt{6}=-6\sqrt{6}\)
NT
29 tháng 8 2021
4. \(A=3\sqrt{2}+4\sqrt{8}-\sqrt{18}=3\sqrt{2}+8\sqrt{2}=3\sqrt{2}=8\sqrt{2}\)
5. \(\dfrac{\sqrt{12}-\sqrt{48}-\sqrt{108}-\sqrt{192}}{2\sqrt{3}}=\dfrac{2\sqrt{3}-4\sqrt{3}-6\sqrt{3}-8\sqrt{3}}{2\sqrt{3}}=\dfrac{-16\sqrt{3}}{2\sqrt{3}}=-8\sqrt{3}\)
29 tháng 8 2021
4: Ta có: \(A=3\sqrt{2}+4\sqrt{8}-\sqrt{18}\)
\(=3\sqrt{2}+8\sqrt{2}-3\sqrt{2}\)
\(=8\sqrt{2}\)
5: Ta có: \(\left(\sqrt{12}-\sqrt{48}-\sqrt{108}-\sqrt{192}\right):2\sqrt{3}\)
\(=\left(2\sqrt{3}-4\sqrt{3}-6\sqrt{3}-8\sqrt{3}\right):2\sqrt{3}\)
\(=-16\sqrt{3}:2\sqrt{3}=-8\)
13 tháng 12 2021
\(a,=\left(2\sqrt{6}-4\sqrt{3}\right)\sqrt{6}+12\sqrt{2}=12-12\sqrt{2}+12\sqrt{2}=12\\ b,=\dfrac{6\left(3-\sqrt{3}\right)}{6}+\sqrt{3}=3-\sqrt{3}+\sqrt{3}=3\)
6 tháng 6 2021
Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...
NM
24 tháng 8 2017
\(B=\sqrt{18-4\sqrt{15}-4\sqrt{3}+2\sqrt{5}}-\sqrt{13-4\sqrt{3}}\)
\(=\sqrt{12+5+1-4\sqrt{15}-4\sqrt{3}+2\sqrt{5}}-\sqrt{12+1-4\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{5}+1-2\sqrt{3}\right)^2}-\sqrt{\left(2\sqrt{3}-1\right)^2}\)
\(=2\sqrt{3}-1-\sqrt{5}-2\sqrt{3}+1=-\sqrt{5}\)
B1
23 tháng 8 2017
Bạn ko nói rõ lớp mấy để đưa ra cách giải phù hợp.
1) Gọi chữ số hàng đơn vị là x (0 < x <9) => chữ số hàng chục là 3x
Số ban đầu có dạng 10.3x + x = 31x
Sau khi đổi chỗ số mới có dạng 10.x + 3x = 13x
Vì số mới nhỏ hơn số đã cho 18 nên có pt 31x - 13x = 18 <=> 18x = 18 => x = 1 (TMĐK)
Suy ra chữ số hàng chục là 3. Vậy số cần tìm là 31.
2) Tóm tắt thôi nhé.
Chữ số hàng chục là a, hàng đơn vị là b. => Số có dạng 10a + b và a+ b = 10
Số mới sau khi đổi chỗ là 10b + a
Giải hệ 2 pt: a + b = 10 và (10a + b) - (10b + a) = 36
được a = 7; b = 3. Vậy số cần tìm là 73.
3) Gọi a là số tự nhiên sau khi đã xóa đi 5. Số ban đầu là 10a + 5
xóa chữ số 5 thì số ấy giảm đi 1787 đơn vị nên ta có pt : 10a + 5 - 1787 = a
=> 9a = 1782 => a = 198 => Số ban đầu là 1985
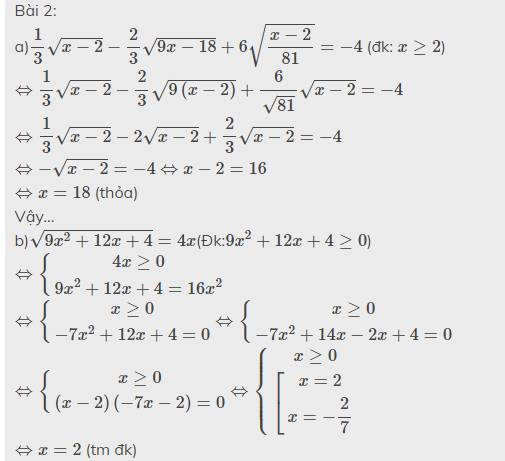
X*3069=3069
X=3069/3069
X-1
X = 3069/3069
X = 1
k cho minh nha