
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: Ta có: \(9x^2+6x-8=0\)
\(\Leftrightarrow9x^2+12x-6x-8=0\)
\(\Leftrightarrow\left(3x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
e: Ta có: \(x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
f: Ta có: \(5x\left(x-3\right)-x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)

\(\left(x+4\right)\left(x-4\right)-x\left(x+6\right)=8\)
\(\Leftrightarrow x^2-16-x^2-6x=8\)
\(\Leftrightarrow-6x=24\Leftrightarrow x=-4\)
\(\left(x+4\right)\left(x-4\right)-x\left(x+6\right)=8\)
\(\Leftrightarrow x^2-16-x^2-6x=8\)
\(\Leftrightarrow-6x=24\)
hay x=-4

1.
$x(x+2)(x+4)(x+6)+8$
$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$
$=a(a+8)+8$ (đặt $x^2+6x=a$)
$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$
Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$
2.
$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$
$=5-(x^2+5x-6)(x^2+5x+6)$
$=5-[(x^2+5x)^2-6^2]$
$=41-(x^2+5x)^2\leq 41$
Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$


\(1,\)
\(2x\left(x-3\right)-\left(3-x\right)=0\)
\(\Leftrightarrow2x\left(x-3\right)+\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=3\end{cases}}\)
\(2,\)
\(3x\left(x+5\right)-6\left(x+5\right)=0\)
\(\Leftrightarrow\left(3x-6\right)\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x-6=0\\x+5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-5\end{cases}}\)
\(3,\)
\(x^4-x^2=0\)
\(\Leftrightarrow x^2\left(x^2-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=0\\x^2-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm1\end{cases}}\)
\(4,\)
\(x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
\(5,\)
\(x\left(x+6\right)-10\left(x-6\right)=0\)
\(\Leftrightarrow x^2+6x-10x+60=0\)
\(\Leftrightarrow x^2-4x+60=0\)
\(\Leftrightarrow x^2-4x+4+56=0\)
\(\Leftrightarrow\left(x-2\right)^2=-56\)(Vô lý)
=> Phương trình vô nghiệm

Ta có : \(B\left(x\right)=x^4-x^2-6=0\)
\(\Leftrightarrow x^4-3x^2+2x^2-6=0\Leftrightarrow x^2\left(x^2-3\right)+2\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x^2+2>0\right)\left(x^2-3\right)=0\Leftrightarrow x=\pm\sqrt{3}\)
\(C\left(x\right)=x^4-5x^2+4=0\)
\(\Leftrightarrow x^4-4x^2-x^2+4=0\Leftrightarrow x^2\left(x^2-4\right)-\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)=0\Leftrightarrow x=1;-1;2;-2\)

=>(x-6)^4+(x-8)^4=16
Đặt a=x-7
=>(a-1)^4+(a+1)^4=16
=>a^4+4a^3+6a^2+4a+1+a^4-4a^3+6a^2-4a+1=16
=>2a^4+12a^2-14=0
=>a^4+6a^2-7=0
=>(a^2+7)(a^2-1)=0
=>a^2=1
=>a=1 hoặc a=-1
=>x-7=1 hoặc x-7=-1
=>x=6 hoặc x=8

=>(x-6)^4+(x-8)^4=16
Đặt a=x-7
=>(a-1)^4+(a+1)^4=16
=>a^4+4a^3+6a^2+4a+1+a^4-4a^3+6a^2-4a+1=16
=>2a^4+12a^2-14=0
=>a^4+6a^2-7=0
=>(a^2+7)(a^2-1)=0
=>a^2=1
=>a=1 hoặc a=-1
=>x-7=1 hoặc x-7=-1
=>x=6 hoặc x=8
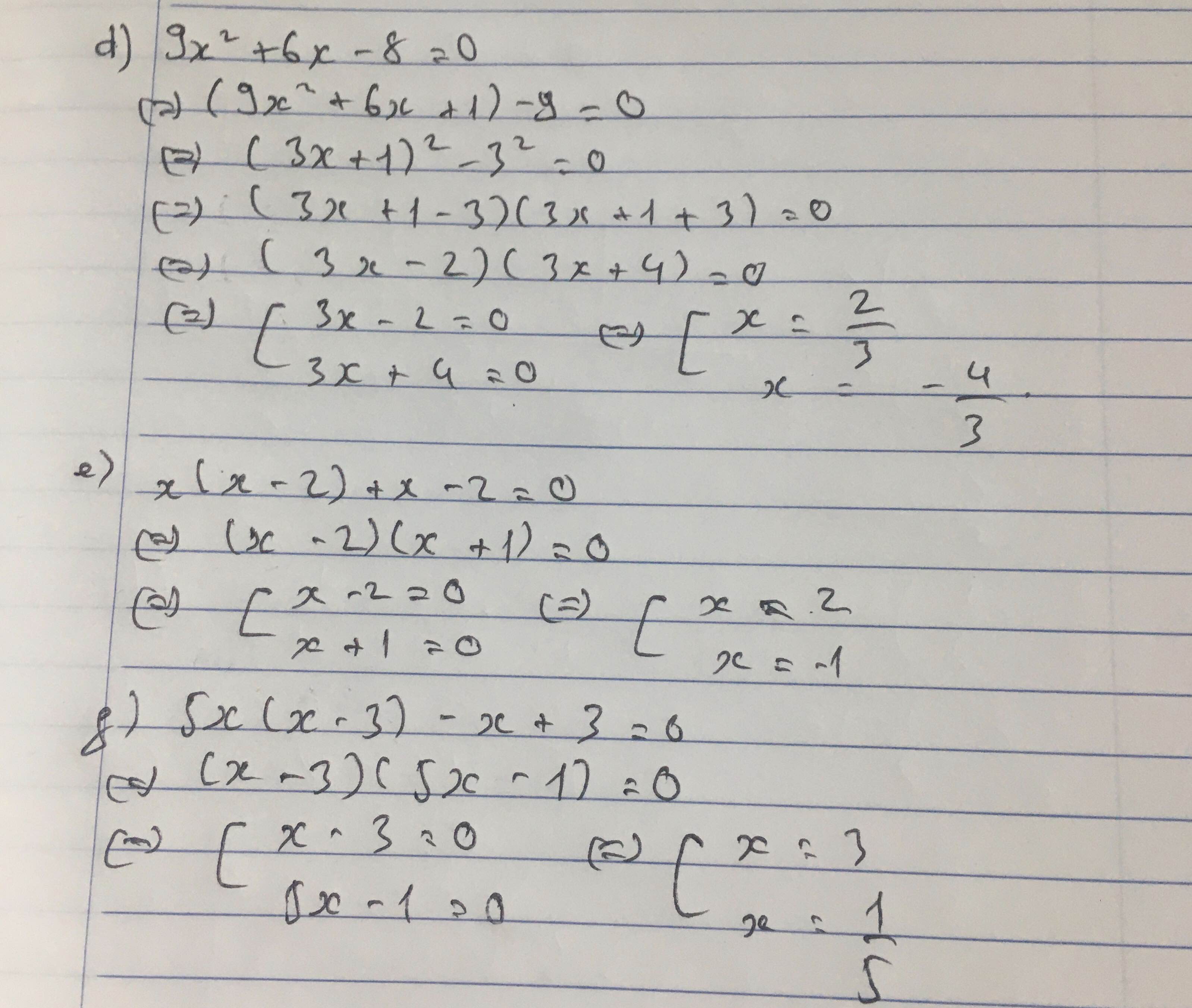 Mình trình bày trong hình ^^ Bn tham khảo nhé
Mình trình bày trong hình ^^ Bn tham khảo nhé
\(\left(x-6\right)\left(x-6\right)-x\left(x-4\right)=4\)
\(\Leftrightarrow x^2-12x+36-x^2+4x=4\)
\(\Leftrightarrow36-8x=4\)
\(\Leftrightarrow8x=36-4\)
\(\Leftrightarrow8x=32\)
\(\Leftrightarrow x=32:8\)
\(\Leftrightarrow x=4\)
\(\left(x-6\right)\left(x-6\right)-x\left(x-4\right)=4\)
\(x^2-6^2-x^2-4x=4\)
\(6^2-4x=4\)
\(4x=36+4\)
\(4x=40\)
\(x=10\)