
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: |x-5|=x-5 <=> x-5 > 0 <=>x > 5
|x-5|=-(x-5) <=> x-5 < 0 <=>x < 5
+)x > 5 thì x-5-x=3=>-5=3 => loại
+)x < 5 thì -(x-5)-x=3<=>-x+5-x=3 <=>-2x+5=3<=>-2x=-2<=>x=1 (TM)
Vậy x=1
a)x(3x-5)-9x+15=0<=>3x^2-14x+15=0 (lấy máy tính ra bấm,nếu ko cho dùng máy tính lập delta giải)
b)x^2(2x-3)-8x+12=0<=>2x^3-3x^2-8x+12=...
c)5x^3-7x^2-15x+21=0
d)(x-3)^2=4x^2-20x+25<=>3x^2-14X+16=0
e)(x-1)^2-5=(x+2)(x-2)-x(x-1)<=>x^2-2x...
<=>x^2-3x=0
f)(2x-3)^3-(2x+3)(4x^2-1)=0<=>8x^3+27-...


1377:x=9(x+27)
\(\Rightarrow1377:x\cdot x=\left[9\left(x+27\right)\right]\cdot x\)
\(\Rightarrow1377=\left[9x+243\right]x\)
\(\Rightarrow1377=9x^2+243x\)
\(\Rightarrow-9\left(x^2+27x-153\right)=0\)
\(\Rightarrow x^2+27x-153=0\)
\(\Delta=27^2-\left(-4\left(1.153\right)\right)=1341\)
\(\Rightarrow x_{1,2}=\frac{-27\pm\sqrt{1341}}{2}\)

Áp dụng bất đẳng thức Cô-si với số x>0
Ta có :
\(x + \dfrac{1}{x} \geq 2\sqrt{x. \dfrac{1}{x}} = 2.\sqrt{1} = 2\)
Vậy min của A là 2 khi \(x = \dfrac{1}{x} \Leftrightarrow x = 1\)


Nếu toàn bộ các kí hiệu đều đúng thì hợp lại chúng ta sẽ được \(x\ne1\) hay viết cách khác là \(x\in\left(-\infty;1\right)\cup\left(1;+\infty\right)\) hoặc \(x\in R\backslash\left\{1\right\}\)

Bài 1:
a)\(\begin{cases}\left(x-3\right)^2+\left(y+2\right)^2=0\\\begin{cases}\left(x-3\right)^2\ge0\\\left(y+2\right)^2\ge0\end{cases}\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-3\right)^2=0\\\left(y+2\right)^2=0\end{cases}\)\(\Rightarrow\begin{cases}x=3\\y=-2\end{cases}\)
b) tương tự
b) (x-12+y)200+(x-4-y)200= 0
\(\begin{cases}\left(x-12+y\right)^{200}+\left(x-4-y\right)^{200}=0\\\begin{cases}\left(x-12+y\right)^{200}\ge0\\\left(x-4-y\right)^{200}\ge0\end{cases}\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-12+y\right)^{200}=0\\\left(x-4-y\right)^{200}=0\end{cases}\)\(\Rightarrow\begin{cases}x-12+y=0\\x-4-y=0\end{cases}\)\(\Rightarrow\begin{cases}x+y=12\left(1\right)\\x-y=4\left(2\right)\end{cases}\)
Trừ theo vế của (1) và (2) ta được:
\(2y=8\Rightarrow y=4\)\(\Rightarrow\begin{cases}x+4=12\\x-4=4\end{cases}\)\(\Rightarrow x=8\)
Vậy x=8; y=4

Ta có 3*\x+1\+1=28
3*\x+1\=28-1
3*\x+1\=27
\x+1\=27:3
\x+1\=9
=>x+1=9 hoặc x+1=-9
x=9-1 x=-9-1
x=8 x=-10
Vậy x=8 hoặc x=-10

Lời giải:
Dễ thấy $x,y$ không âm và $x\geq 3$
Nếu $y=0$ thì $x=3$ (thỏa mãn)
Nếu $y\geq 1$:
$2^x=3^y+7\equiv 1\pmod 3$
$\Leftrightarrow (-1)^x\equiv 1\pmod 3\Rightarrow x$ chẵn.
Với $x\geq 3$ thì $3^y=2^x-7\equiv 1\pmod 4$
$\Leftrightarrow (-1)^y\equiv 1\pmod 4\Rightarrow y$ chẵn.
Đặt $x=2a; y=2b$ với $a,b$ là số tự nhiên.
Khi đó: $(2^a-3^b)(2^a+3^b)=7$
$\Rightarrow 2^a-3^b=1; 2^a+3^b=7$
$\Rightarrow 2^{a+1}=8\Rightarrow a=2$ kéo theo $b=1$
$\Rightarrow x=4; y=2$
Vậy $(x,y)=(3,0); (4,2)$
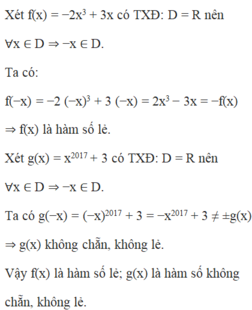


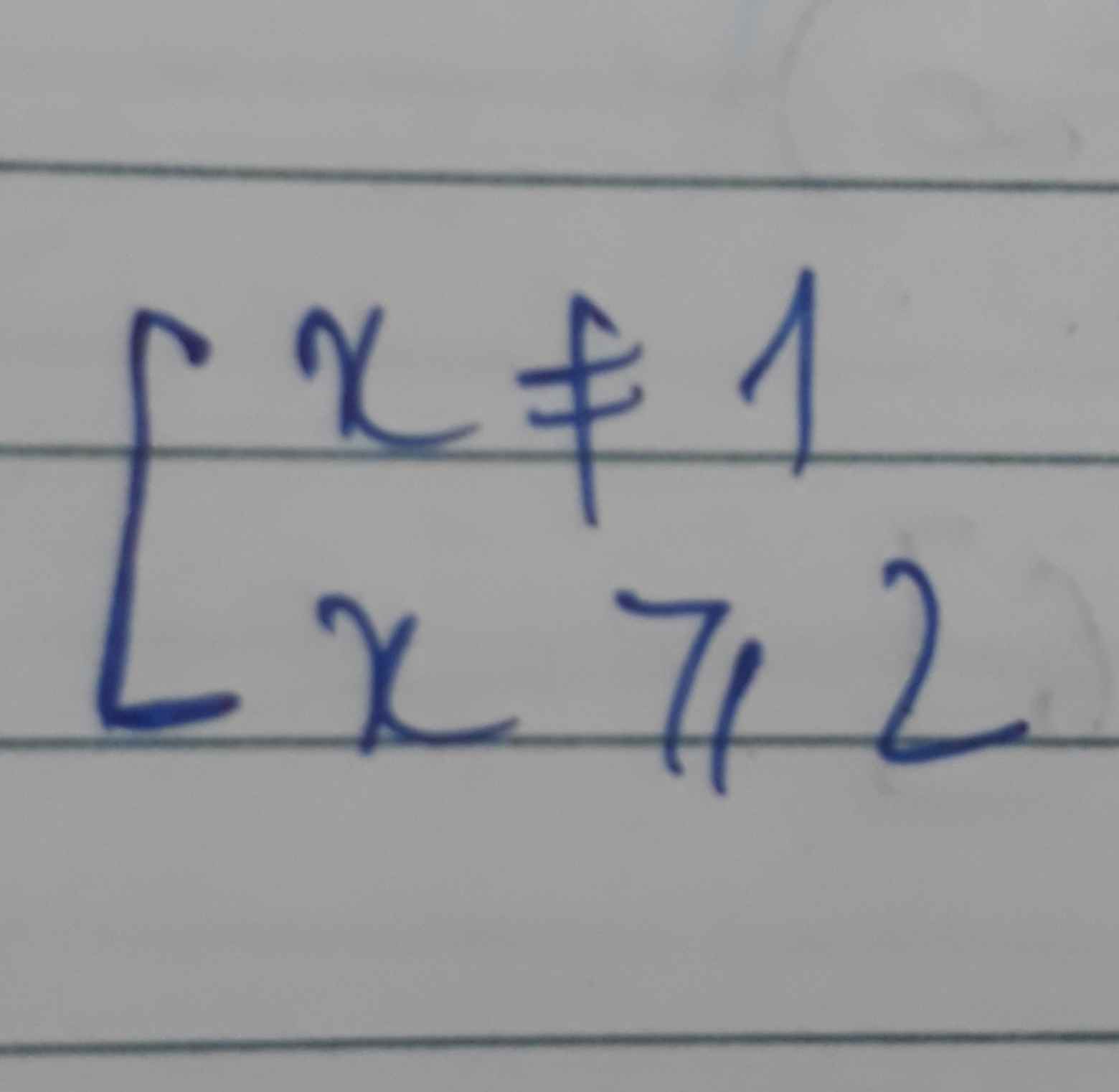
\(x^{2017}=x^{2016}\)
\(\Leftrightarrow x^{2017}-x^{2016}=0\)
\(\Leftrightarrow x^{2016}\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^{2016}=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy x = 0 hoặc x = 1