
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{5^{x+1}}{125}=\dfrac{1}{25^{x-2}}\\ \dfrac{5^{x+1}}{125}=\dfrac{1}{5^{2x-4}}\\ 5^{x+1}\cdot5^{2x-4}=125\\ 5^{x+1+2x-4}=5^3\\ 5^{\left(x+2x\right)+\left(1-4\right)}=5^3\\ 5^{3x-3}=5^3\\ 3x-3=3\\ 3x=6\\ x=2\)

a) \(\dfrac{2}{3}x-\dfrac{1}{2}x=\left(-\dfrac{7}{12}\right)\cdot1\dfrac{2}{5}\)
\(\Rightarrow\dfrac{1}{6}x=\left(-\dfrac{7}{12}\right)\cdot\dfrac{7}{5}\)
\(\Rightarrow\dfrac{1}{6}x=-\dfrac{49}{60}\)
\(\Rightarrow x=-\dfrac{49}{60}:\dfrac{1}{6}\)
\(\Rightarrow x=-\dfrac{49}{10}\)
b) \(\left(\dfrac{1}{5}-\dfrac{3}{2}x\right)^2=\dfrac{9}{4}\)
\(\Rightarrow\left(\dfrac{1}{5}-\dfrac{3}{2}x\right)^2=\left(\pm\dfrac{3}{2}\right)^2\)
+) \(\dfrac{1}{5}-\dfrac{3}{2}x=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{3}{2}x=\dfrac{1}{5}-\dfrac{3}{2}\)
\(\Rightarrow\dfrac{3}{2}x=-\dfrac{13}{10}\)
\(\Rightarrow x=-\dfrac{13}{10}:\dfrac{3}{2}\)
\(\Rightarrow x=-\dfrac{13}{15}\)
+) \(\left(1,25-\dfrac{4}{5}x\right)^3=-125\)
\(\Rightarrow\left(\dfrac{5}{4}-\dfrac{4}{5}x\right)^3=\left(-5\right)^3\)
\(\Rightarrow\dfrac{5}{4}-\dfrac{4}{5}x=-5\)
\(\Rightarrow\dfrac{4}{5}x=\dfrac{5}{4}+5\)
\(\Rightarrow\dfrac{4}{5}x=\dfrac{25}{4}\)
\(\Rightarrow x=\dfrac{25}{4}:\dfrac{4}{5}\)
\(\Rightarrow x=\dfrac{125}{16}\)
a, \(\dfrac{2}{3}\)\(x\) - \(\dfrac{1}{2}\)\(x\) = (- \(\dfrac{7}{12}\)). 1\(\dfrac{2}{5}\)
\(x\).(\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) = (- \(\dfrac{7}{12}\)) . \(\dfrac{7}{5}\)
\(x\). \(\dfrac{1}{6}\) = - \(\dfrac{49}{60}\)
\(x\) = - \(\dfrac{49}{60}\).6
\(x\) = -\(\dfrac{49}{10}\)

a, \(\dfrac{3}{7}\)\(x\)- \(\dfrac{2}{3}\)\(x\) = \(\dfrac{10}{21}\)
(\(\dfrac{3}{7}\) - \(\dfrac{2}{3}\)) \(\times\) \(x\) = \(\dfrac{10}{21}\)
- \(\dfrac{5}{21}\) \(\times\) \(x\) = \(\dfrac{10}{21}\)
\(x\) = \(\dfrac{10}{21}\) : (-\(\dfrac{5}{21}\))
\(x\) = -2
b, \(\dfrac{7}{35}\) : (\(x-\dfrac{1}{3}\)) = - \(\dfrac{2}{25}\)
\(x\) - \(\dfrac{1}{3}\) = \(\dfrac{7}{35}\) : (- \(\dfrac{2}{25}\))
\(x\) - \(\dfrac{1}{3}\) = - \(\dfrac{5}{2}\)
\(x\) = - \(\dfrac{5}{2}\) + \(\dfrac{1}{3}\)
\(x\) = - \(\dfrac{13}{6}\)
c, 3.(\(x\) - \(\dfrac{1}{2}\)) - 5.(\(x\) + \(\dfrac{3}{5}\)) = - \(x\)+ \(\dfrac{1}{5}\)
3\(x\) - \(\dfrac{3}{2}\) - 5\(x\) - 3 = - \(x\) + \(\dfrac{1}{5}\)
- \(x\) + 5\(x\) - 3\(x\) = - \(\dfrac{3}{2}\) - 3 - \(\dfrac{1}{5}\)
\(x\) = - \(\dfrac{47}{10}\)
\(a,\dfrac{3}{7}x-\dfrac{2}{3}x=\dfrac{10}{21}\\ \Rightarrow x\left(\dfrac{3}{7}-\dfrac{2}{3}\right)=\dfrac{10}{21}\\ \Rightarrow x.-\dfrac{5}{21}=\dfrac{10}{21}\\ \Rightarrow x=-2\\ b,\dfrac{7}{35}:\left(x-\dfrac{1}{3}\right)=-\dfrac{2}{25}\\ \Rightarrow\dfrac{1}{5}:\left(x-\dfrac{1}{3}\right)=-\dfrac{2}{25}\\ \Rightarrow x-\dfrac{1}{3}=-\dfrac{5}{2}\\ \Rightarrow x=-\dfrac{13}{6}\\ c,3.\left(x-\dfrac{1}{2}\right)-5.\left(x+\dfrac{3}{5}\right)=-x+\dfrac{1}{5}\\ \Rightarrow3x-\dfrac{3}{2}-5x+5=-x+\dfrac{1}{5}\)
\(\Rightarrow x\left(3-5\right)-\dfrac{3}{2}+5=-x+\dfrac{1}{5}\\ \Rightarrow-2x-\dfrac{13}{2}=-x+\dfrac{1}{5}\\ \Rightarrow-x-\dfrac{13}{5}=\dfrac{1}{5}\\ \Rightarrow x=\dfrac{1}{5}-\dfrac{13}{5}\\ \Rightarrow x=-\dfrac{12}{5}.\)

a: \(\Leftrightarrow7^x\cdot49+7^x\cdot\dfrac{2}{7}=345\)
\(\Leftrightarrow7^x=7\)
hay x=1
c: \(\left(\dfrac{1}{3}-\dfrac{1}{2}\right)^{x-1}=\dfrac{1}{36}\)
\(\Leftrightarrow\left(-\dfrac{1}{6}\right)^{x-1}=\left(-\dfrac{1}{6}\right)^2\)
=>x-1=2
hay x=3
d: \(\dfrac{25}{5^x}=\dfrac{1}{125}\)
\(\Leftrightarrow5^x=5^2\cdot5^3=5^5\)
hay x=5

\(\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+...+\dfrac{1}{x\left(x+3\right)}=\dfrac{125}{376}\)
\(\Leftrightarrow\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{x}-\dfrac{1}{x+3}\right)=\dfrac{125}{376}\)
\(\Leftrightarrow\dfrac{1}{3}\left(1-\dfrac{1}{x+3}\right)=\dfrac{125}{376}\left(x\ne0;x\ne-3\right)\)
\(\Leftrightarrow\dfrac{x+3-1}{x+3}=\dfrac{3.125}{376}\Leftrightarrow\dfrac{x+2}{x+3}=\dfrac{3.125.}{376}.\dfrac{\left(x+3\right)}{x+3}\)
\(\Leftrightarrow376\left(x+2\right)=3.125.\left(x+3\right)\)
\(\Leftrightarrow376x+752=375x+1125\)
\(\Leftrightarrow376x-375x=1125-752\Leftrightarrow x=373\left(x\in N^{\cdot}\right)\)

Bài 2:
\(\Leftrightarrow\left\{{}\begin{matrix}3^{3x-2x+y}=3^5\\5^{2x-x-y}=5^3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\x-y=3\end{matrix}\right.\)
=>x=1;y=-2

a) \(\left(\dfrac{1}{3}-\dfrac{1}{2}\right)^x-1=\dfrac{1}{36}\)
\(\Rightarrow\left(\dfrac{1}{6}\right)^x=1\dfrac{1}{36}\)
\(\Rightarrow x=2\)
b) \(\dfrac{25}{5x}=\dfrac{1}{125}\)
\(\Rightarrow25\cdot125=5x\)
\(\Rightarrow5^2\cdot5^3=5^x\)
\(\Rightarrow x=5\)
Bn Đời về cơ bản là buồn... cười!!! nhìn sai đề ở ý a .
a) \(\left(\dfrac{1}{3}-\dfrac{1}{2}\right)^{x-1}=\dfrac{1}{36}\)
\(\Leftrightarrow\left(-\dfrac{1}{6}\right)^{x-1}=\dfrac{1}{36}\)
\(\Leftrightarrow\left(-\dfrac{1}{6}\right)^{x-1}=\dfrac{1}{6}^2\)
\(\Leftrightarrow x-1=2\Rightarrow x=3\)
b) \(\dfrac{25}{5^x}=\dfrac{1}{125}\Leftrightarrow\dfrac{25}{5^x}=\dfrac{25}{3125}\Leftrightarrow\dfrac{25}{5^x}=\dfrac{25}{5^5}\Rightarrow x=5\)
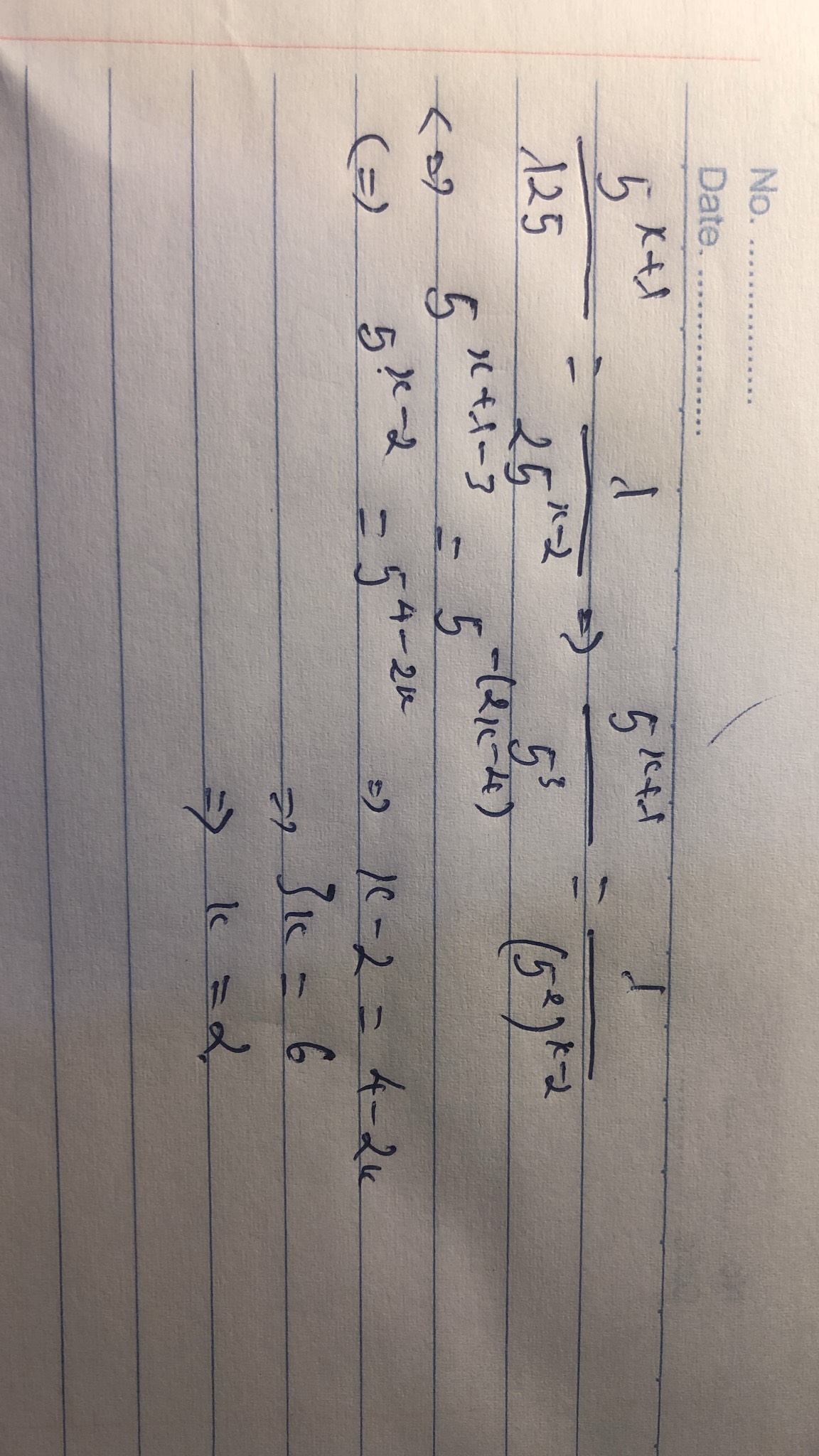
Áp dụng tính chất tỉ lệ thức, ta có: \(\dfrac{25}{5^x}=\dfrac{1}{125}\)
\(\Rightarrow25.125=5^x\)
\(\Rightarrow5^2.5^3=5^x\)
\(\Rightarrow x=5\)
Vậy x = 5
\(\dfrac{25}{5^x}=\dfrac{1}{125}\)
= 25 . 125 = 5x
=> 52 . 53 = 5x
<=> 5x =52.53
=> 5x = 55
=> x = 5