K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
3 tháng 12 2018
a, 3 x + 1 : 3 4 = 81
3 x - 3 = 3 4
x – 3 = 4
x = 7
Vậy x = 7
b, 3 x + 3 . 3 x + 1 = 729
3 2 x + 4 = 3 6
2x + 4 = 6
x = 1
Vậy x = 1
c, 2 x + 3 . 2 x = 128
2 2 x + 3 = 2 7
2x + 3 = 7
x = 2
Vậy x = 2
d, 23 + 3 x = 5 6 : 5 3
23 + 3 x = 5 3
23 + 3x = 125
3x = 102
x = 34
Vậy x = 34
e, 2 x + 2 x + 4 = 272
2 x + 2 x . 2 4 = 272
2 x ( 1 + 2 4 ) = 272
2 x . 17 = 272
2 x = 16
2 x = 2 4
x = 4
Vậy x = 4
PT
1
CM
29 tháng 10 2019
− 3 29 − 2 29 ≤ x 29 < 5 29 − 7 29 . ⇒ − 5 29 ≤ x 29 < − 2 29 ⇒ − 5 ≤ x < − 2 ⇒ x ∈ − 5 ; − 4 ; − 3
TM
1
NM
Nguyễn Minh Quang
Giáo viên
10 tháng 12 2021
ta có :
\(\left(x+5\right)^2\in\left\{13^2,18^2,24^2,27^2\right\}\)
nên \(x+5\in\left\{-27,-24,-18,-13,13,18,24,27\:\right\}\)
hay \(x\in\left\{-32.-29.-23.-18,8,13,19,22\right\}\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 8 2023
\(1\le3^{n+2}\le729\)
\(\Rightarrow3^0\le3^{n+2}\le3^6\)
\(\Rightarrow0\le n+2\le6\)
\(\Rightarrow0-2\le n\le6-2\)
\(\Rightarrow-2\le n\le4\)
Mà: \(n\in N^+\)
\(\Rightarrow0\le n\le4\)
\(\Rightarrow n\in\left\{0;1;2;3;4\right\}\)
KV
30 tháng 8 2023
Sửa đề:
1 ≤ 3ⁿ⁺² ≤ 729
3⁰ ≤ 3ⁿ⁺² ≤ 3⁶
0 ≤ n + 2 ≤ 6
-2 ≤ n ≤ 4
Do n ∈ ℕ
⇒ n ∈ {0; 1; 2; 3; 4}
27 tháng 8 2023
\(1\le3^{n+1}\le729\) \(\left(n\inℕ\right)\)
\(\Rightarrow3^0\le3^{n+1}\le3^6\)
\(\Rightarrow0\le n+1\le6\)
\(\Rightarrow-1\le n\le5\)
\(\Rightarrow n\in\left\{0;1;2;3;4;5\right\}\)
26 tháng 8 2021
3^{x}.3^{x+1}.3^{x+2}>=729`
`=>3^{x+x+1+x+2}>=3^6`
`=>3^{3x+3}>=3^6`
`=>3x+3>=6`
`=>3x>=3=>x>=1`
KL
1
24 tháng 1 2017
7) ( 2x2+ 1)3= 729
=> ( 2x2+ 1)3 = 36
=> ( 2x2+ 1)3= 93
=> 2x2+ 1= 9
=> 2x2= 8
=> x2= 4
=> x= 2
8) ( 3x2- 43)3= 125
=> (3x2- 43)3= 53
=> 3x2- 43= 5
=> 3x2= 48
=> x2= 16
=> x= 4
Vậy x=4
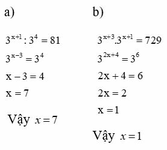
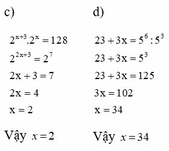
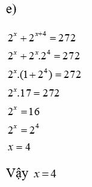
3x = 729
<=> 3x = 36
=> x = 6
\(3^x=729\Rightarrow x=6\)