K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 1 2022
a: =>(x+10)(x-1)=0
=>x=-10 hoặc x=1
b: \(A=x^3-1-\left(x+5\right)\left(x^2-3\right)-5x^2-10x-5\)
\(=x^3-5x^2-10x-6-x^3+3x-5x^2+15\)
=-7x+9
=110/13
11 tháng 4 2021
a, \(A=\left(\frac{x}{x^2-4}+\frac{2}{2-x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)ĐK : \(x\ne\pm2\)
\(=\left(\frac{x-2\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}\right):\left(\frac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)
\(=\frac{x-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}:\frac{x^2-4+10-x^2}{x+2}=\frac{-6}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{6}=\frac{-1}{x-2}\)
b, Ta có : \(2\left|x\right|=1\Leftrightarrow\left|x\right|=\frac{1}{2}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
TH1 : Thay x = 1/2 vào biểu thức A ta được : \(-\frac{1}{\frac{1}{2}+2}=-\frac{1}{\frac{5}{2}}=-\frac{2}{5}\)
TH2 : Thay x = -1/2 vào biểu thức A ta được : \(\frac{-1}{-\frac{1}{2}-2}=-\frac{1}{-\frac{5}{2}}=-1.\left(-\frac{2}{5}\right)=\frac{2}{5}\)
c, Ta có A < 0 hay \(\frac{-1}{x-2}< 0\Rightarrow x-2>0\)do - 1 < 0
\(\Leftrightarrow x>2\)
d, Ta có A = x hay \(\frac{-1}{x-2}=x\Rightarrow x^2-2x=-1\Leftrightarrow\left(x-1\right)^2=0\Leftrightarrow x=1\)
DX
26 tháng 2 2023
\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(\Rightarrow A=\left(\dfrac{x-2\left(x+2\right)+1\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)
\(\Rightarrow A=\left(\dfrac{-6}{x^2-4}\right):\left(\dfrac{6}{x+2}\right)\)
\(\Rightarrow A=-\dfrac{6}{x^2-4}.\dfrac{x+2}{6}=-\dfrac{6\left(x+2\right)}{\left(x-2\right)\left(x+2\right)6}=-\dfrac{1}{x-2}\)
để A<0 thì :
\(\left\{{}\begin{matrix}x-2\ne0\\x-2\notin Z-\end{matrix}\right.\)\(\Leftrightarrow x\in\left\{3;4;5;6;7;8;9;....n\right\}\)
( Z- là tập hợp số nguyên âm )
Để A có giá trị nguyên thì :
\(\left\{{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
9 tháng 1 2022
\(a,\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=0\\ \Rightarrow\left(x^3-27\right)+x\left(4-x^2\right)=0\\ \Rightarrow x^3-27+4x-x^3=0\\ \Rightarrow4x-27=0\\ \Rightarrow4x=27\\ \Rightarrow x=\dfrac{27}{4}\)
\(b,\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\\ \Rightarrow\left(x^3+3x^2+3x+1\right)-\left(x^3-3x^2+3x-1\right)-6\left(x^2-2x+1\right)=-10\\ \Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+10=0\)
\(\Rightarrow12x+6=0\\ \Rightarrow12x=-6\\ \Rightarrow x=-\dfrac{1}{2}\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 8 2023
\(2\left(x-1\right)-5\left(x+2\right)=-10\\ \Leftrightarrow2x-2-5x-10=-10\\ \Leftrightarrow-3x=2\\ \Leftrightarrow x=-\dfrac{2}{3}\)
NT
0
QN
5
20 tháng 7 2017
\(\text{a , (x-3).(x^2+3x+9)+x(x+2).(2-x)=1 }\)
=(x3-33)+x(4-x2)=1
=x3-27+4x-x3=1
4x-27=1
4x=28
x=7
\(\text{b, (x+1)^3-(x-1)^3-6.(x-1)^2=-10}\)
=-0,5
23 tháng 5 2018
\(A=x^2-2x+10\)
\(A=\left(x^2-2x+1\right)+9\)
\(A=\left(x-1\right)^2+9\)
Mà \(\left(x-1\right)^2\ge0\)
\(\Rightarrow A\ge9\)
Dấu "=" xảy ra khi :
\(x-1=0\Leftrightarrow x=1\)
Vậy Min A = 9 khi x = 1
23 tháng 5 2018
\(B=x^2-5x-7\)
\(B=\left(x^2-5x+\frac{25}{4}\right)-\frac{53}{4}\)
\(B=\left(x-\frac{5}{2}\right)^2-\frac{53}{4}\)
Mà \(\left(x-\frac{5}{2}\right)^2\ge0\)
\(\Rightarrow B\ge-\frac{53}{4}\)
Dấu "=" xảy ra khi :
\(x-\frac{5}{2}=0\Leftrightarrow x=\frac{5}{2}\)
Vậy \(B_{Min}=-\frac{53}{4}\Leftrightarrow x=\frac{5}{2}\)
28 tháng 11 2018
a, Ta có :
(x-2)^2 - (x-3)(x+3) = 6
=> (x-2)^2 - (x-3)^2 = 6 .
=> [(x-2) - (x-3)]^2 = 6 .
=> [ x - 2 - x + 3 ]^2 = 6 .
=> 0x + 1^2 = 6 .
=> 0x + 1 = 6 .
=> 0x = 5 .
=> Vô lí .
=> Không cos giá trị của x .
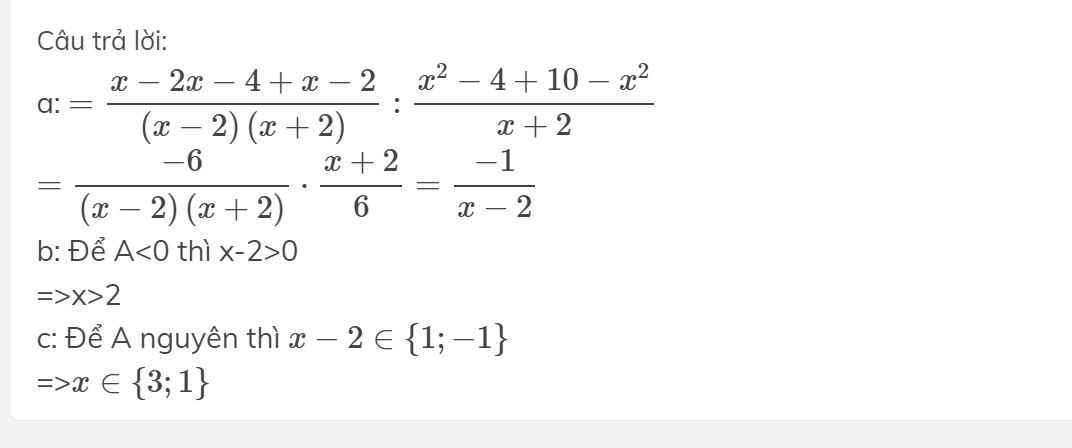
(x + 2)(x - 1) = 10
=> x2 + x - 2 = 10
=> \(\left(x^2+\frac{1}{2}x\right)+\left(\frac{1}{2}x+\frac{1}{4}\right)-\frac{9}{4}=10\)
=> \(\left(x+\frac{1}{2}\right)^2=\frac{49}{4}\)
=> \(\left(x+\frac{1}{2}\right)^2=\left(\frac{7}{2}\right)^2\)
=> \(\orbr{\begin{cases}x+\frac{1}{2}=\frac{7}{2}\\x+\frac{1}{2}=-\frac{7}{2}\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=-4\end{cases}}\)
( x + 2 )( x - 1 ) = 10
<=> x2 + x - 2 = 10
<=> x2 + x - 2 - 10 = 0
<=> x2 + x - 12 = 0
<=> x2 + 4x - 3x - 12 = 0
<=> ( x2 + 4x ) - ( 3x + 12 ) = 0
<=> x( x + 4 ) - 3( x + 4 ) = 0
<=> ( x - 3 )( x + 4 ) = 0
<=> x - 3 = 0 hoặc x + 4 = 0
<=> x = 3 hoặc x = -4
Vậy S = { 3 ; -4 }