Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, Đổi chỗ 3 viên ở 3 đỉnh tam giác: viên dưới cùng lên đỉnh trên cùng, 2 viên ngoài cùng ở 2 bên đảo xuốn đáy
2, 8-6+2=4; 12-5+8=15; 13-10+15=18. x=15
3,
*) \(5^3+5=130;3^3+3=30;2^3+2=10;1^3+1=2\)
*) 2+3=8 hay 2.(2+3)-2=8
4+5=32 hay 4.(4+5)-4=32
5+8=60 hay 5.(5+8)-5=60
6+7=72 hay 6.(6+7)-6=72
7+8= 7.(7+8)-7=98

Đặt MA=x \(\Rightarrow\)MB= 24-x với \(x\in\left[0;24\right]\)
Đặt f(x)=MC+MD=\(\sqrt{MA^2+AC^2}+\sqrt{MB^2+BD^2}=\sqrt{x^2+10^2}+\sqrt{\left(24-x^2\right)+30^2}\)
Ta xét hàm f(x) trên đoạn [0;24]
\(f'\left(x\right)=\frac{x}{\sqrt{x^2+10^2}}-\frac{24-x}{\sqrt{\left(24-x\right)^2+30^2}}\\ =\frac{MA}{MC}-\frac{MB}{MD}\)
\(f'\left(x\right)=0\Leftrightarrow\frac{MA}{MC}-\frac{MB}{MD}=0\Leftrightarrow\frac{MA}{MC}=\frac{MB}{MD}\)
từ đó suy ra hai tam giác vuông \(\Delta MAC\) và \(\Delta MBD\) đồng dạng
\(\Rightarrow\frac{MA}{MC}=\frac{MB}{MD}=\frac{AC}{BD}=\frac{1}{3}\)
Vậy \(MA=\frac{24}{3+1}=6\)(m) và MB=24-6=18(m)

gọi a,b,c(cm) lần lượt là số đo 3 chiều của hình hộp
Ta có: \(S_1=a.b\\ S_2=b.c\\ S_3=a.c\)
\(\Rightarrow V=a.b.c=\sqrt{S_1.S_2.S_3}=\sqrt{20.28.35}=140\left(cm^3\right)\)

14.
\(log_aa^2b^4=log_aa^2+log_ab^4=2+4log_ab=2+4p\)
15.
\(\frac{1}{2}log_ab+\frac{1}{2}log_ba=1\)
\(\Leftrightarrow log_ab+\frac{1}{log_ab}=2\)
\(\Leftrightarrow log_a^2b-2log_ab+1=0\)
\(\Leftrightarrow\left(log_ab-1\right)^2=0\)
\(\Rightarrow log_ab=1\Rightarrow a=b\)
16.
\(2^a=3\Rightarrow log_32^a=1\Rightarrow log_32=\frac{1}{a}\)
\(log_3\sqrt[3]{16}=log_32^{\frac{4}{3}}=\frac{4}{3}log_32=\frac{4}{3a}\)
11.
\(\Leftrightarrow1>\left(2+\sqrt{3}\right)^x\left(2+\sqrt{3}\right)^{x+2}\)
\(\Leftrightarrow\left(2+\sqrt{3}\right)^{2x+2}< 1\)
\(\Leftrightarrow2x+2< 0\Rightarrow x< -1\)
\(\Rightarrow\) có \(-2+2020+1=2019\) nghiệm
12.
\(\Leftrightarrow\left\{{}\begin{matrix}x-2>0\\0< log_3\left(x-2\right)< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\1< x-2< 3\end{matrix}\right.\)
\(\Rightarrow3< x< 5\Rightarrow b-a=2\)
13.
\(4^x=t>0\Rightarrow t^2-5t+4\ge0\)
\(\Rightarrow\left[{}\begin{matrix}t\le1\\t\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}4^x\le1\\4^x\ge4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\le0\\x\ge1\end{matrix}\right.\)

a) Ta có ∆' = 1 - 3 = -2.
Vậy nghiệm của phương trình là z1,2 =
b) Ta có ∆ = 9 - 56 = -47.
Vậy nghiệm của phương trình là z1,2 = ;
c) Ta có ∆ = 49 - 4.5.11 = -171.
Vậy nghiệm của phương trình là z1,2 =

Lời giải:
Giả sử \(\log _{3}a=\log_4b=\log_{12}c=\log_{13}(a+b+c)=t\)
\(\Rightarrow 13^t=3^t+4^t+12^t\)
\(\Rightarrow \left ( \frac{3}{13} \right )^t+\left ( \frac{4}{13} \right )^t+\left ( \frac{12}{13} \right )^t=1\)
Xét vế trái , đạo hàm ta thấy hàm luôn nghịch biến nên phương trình có duy nhất một nghiệm \(t=2\)
Khi đó \(\log_{abc}144=\log_{144^t}144=\frac{1}{t}=\frac{1}{2}\)
Đáp án B
cho em hỏi tại sao lại có 3^t +4^t +12^t=13^t. Với lại em không hiểu chỗ tại sao hàm số nghịch biến. Và tại sao từ \(\log_{abc}144=\log144_{144^t}=\dfrac{1}{t}\)

a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)

a) Đặt Z = z2 , ta được phương trình Z2 + Z – 6 = 0
Phương trình này có hai nghiệm là Z1 = 2, Z2 = -3
Vậy phương trình có bốn nghiệm là ± √2 và ± i√3.
b) Đặt Z = z2 , ta được phương trình Z2 + 7Z + 10 = 0
Phương trình này có hai nghiệm là Z1 = -5, Z2 = -2
Vậy phương trình có bốn nghiệm là ± i√2 và ± i√5.

a) 3z2 + 7z + 8 = 0 có Δ = 49 – 4.3.8 = -47
Vậy phương trình có hai nghiệm là: z1,2=−7±i√476z1,2=−7±i476
b) z4 – 8 = 0
Đặt Z = z2, ta được phương trình : Z2 – 8 = 0
Suy ra: Z = ± √8
Vậy phương trình đã cho có 4 nghiệm là: z1,2=±4√8,z3,4=±i4√8z1,2=±84,z3,4=±i84
c) z4 – 1 = 0 ⇔ (z2 – 1)(z2 + 1) = 0
Vậy phương trình đã cho có 4 nghiệm là ±1 và ±i
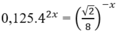








Đáp án : C.