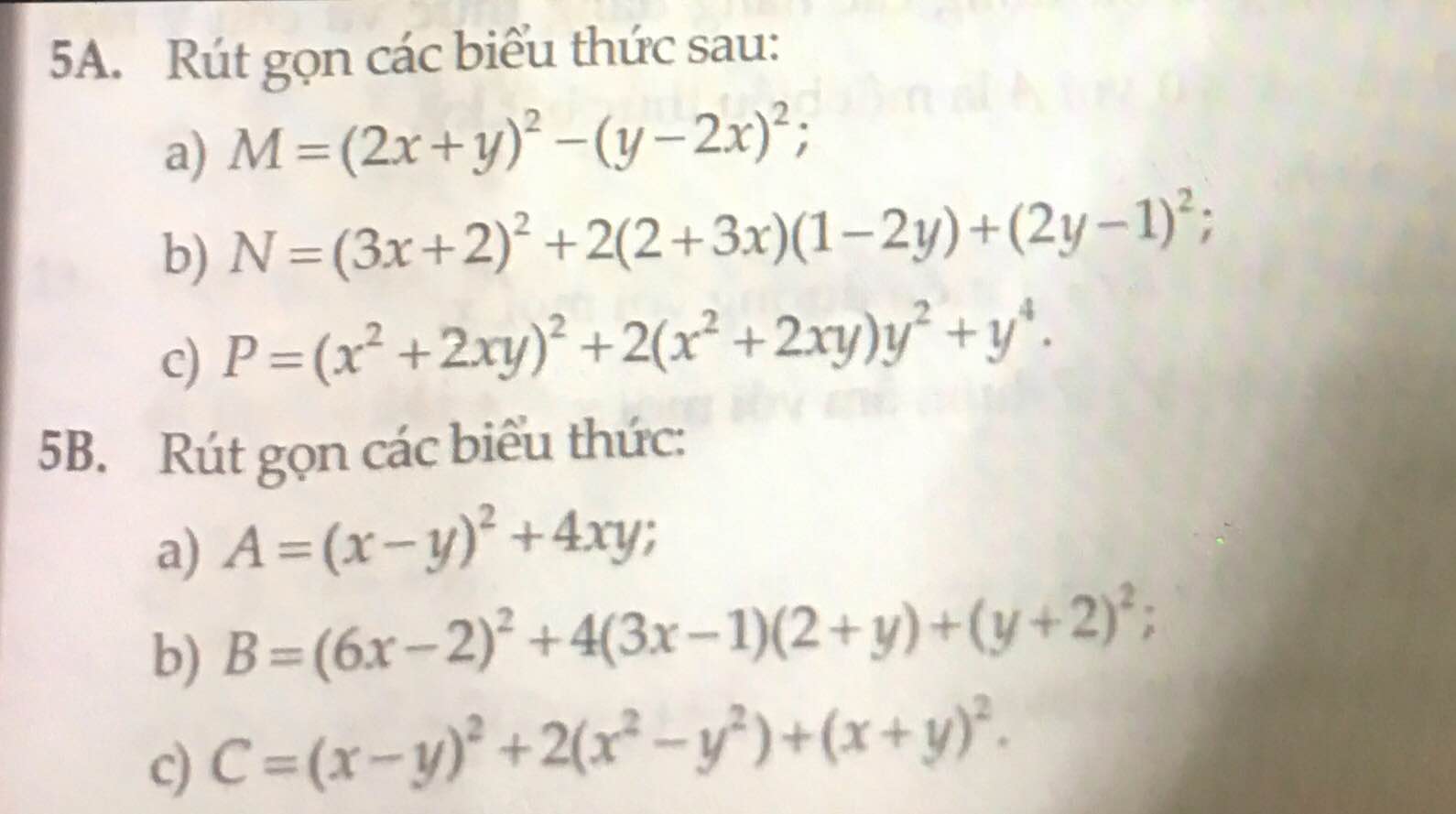Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(5x^{n-2}y^7-8x^{n+2}y^8\right)⋮5x^3y^{n+1}\Leftrightarrow\hept{\begin{cases}n-2\ge3\\7\ge n+1\end{cases}}\Leftrightarrow\orbr{\begin{cases}n=5\\n=6\end{cases}}\)

biểu thức đó = (a-2)(a-1)a(a+1)(a+2)
Trong 5 số nguyên liên tiếp tồn tại 1 số chia hết cho 3, 1 số chia hết cho 5, có 2 số chẵn, trong đó 1 số chia hết cho 2, 1 số chia hết cho 4
Vậy tích của chúng chia hết cho 3.5.2.4= 120
ok nhé bn!!!!! 45436545475966264634657856321423434546545476879


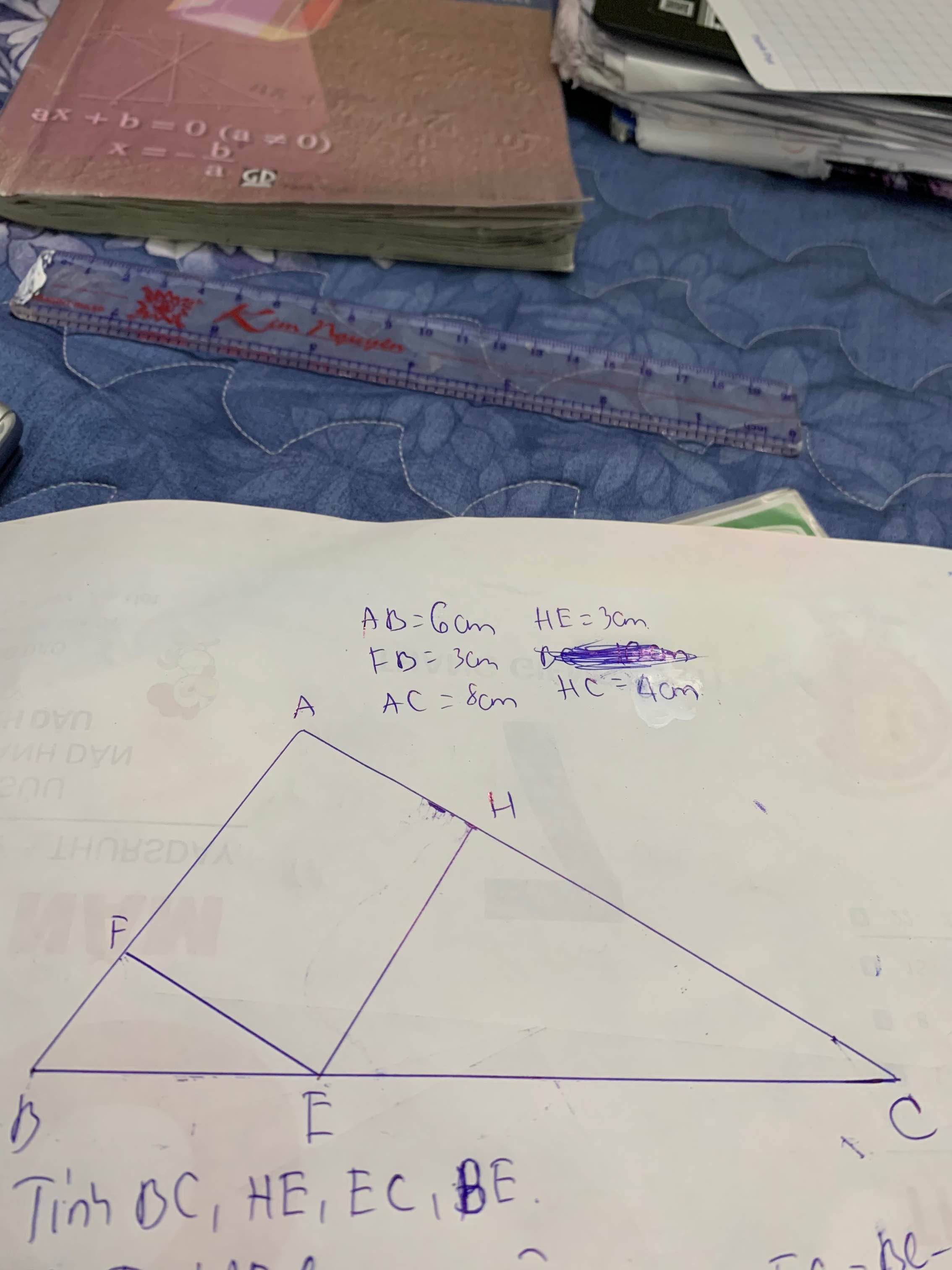
Bài 5A:
a: Ta có: \(M=\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=\left(2x+y-y+2x\right)\left(2x+y+y-2x\right)\)
\(=4x\cdot2y=8xy\)
b: Ta có: \(N=\left(3x+2\right)^2+2\left(3x+2\right)\left(1-2y\right)+\left(2y-1\right)^2\)
\(=\left(3x+2+1-2y\right)^2\)
\(=\left(3x-2y+3\right)^2\)
c: Ta có: \(P=\left(x^2+2xy\right)^2+2\left(x^2+2xy\right)y^2+y^4\)
\(=\left(x^2+2xy+y^2\right)^2\)
\(=\left(x+y\right)^4\)

......................?
mik ko biết
mong bn thông cảm
nha ................

Ta có:
\(n^5-5n^3+4n=n\left(n^4-5n^2+4\right)\)
\(=n\left(n^4-n^2-4n^2+4\right)\)
\(=n\left[n^2\left(n^2-1\right)-4\left(n^2-1\right)\right]\)
\(=n\left(n^2-1\right)\left(n^2-4\right)\)
\(=n\left(n-1\right)\left(n+1\right)\left(n-2\right)\left(n+2\right)\)
\(\Rightarrow\)\(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\)
Vì \(n-2;n-1;;n;n+1;n+2\) là tích của 5 số nguyên liên tiếp chia hết cho 3;5;8
Mà ƯC\(_{\left(3;5;8\right)}\)=1
\(\Rightarrow\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\) chia hết cho:
3.5.8=120(đpcm)