Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tìm số tự nhiên lớn nhất thỏa mãn điều kiện trên, chúng ta cần tìm số tự nhiên lớn nhất mà khi chia cho cả 428 và 708 đều có số dư.
Để làm điều này, chúng ta có thể sử dụng thuật toán Euclid mở rộng. Bắt đầu với hai số 428 và 708, ta thực hiện các bước sau:
1. Tìm ước số chung lớn nhất (GCD) của 428 và 708 bằng cách sử dụng thuật toán Euclid:
- 708 = 428 * 1 + 280
- 428 = 280 * 1 + 148
- 280 = 148 * 1 + 132
- 148 = 132 * 1 + 16
- 132 = 16 * 8 + 4
- 16 = 4 * 4 + 0
GCD của 428 và 708 là 4.
2. Sau đó, chúng ta tìm bội số chung nhỏ nhất (LCM) của 428 và 708 bằng cách sử dụng công thức:
LCM = (428 * 708) / GCD
LCM = (428 * 708) / 4 = 151,704
Vậy số tự nhiên lớn nhất mà khi chia cho cả 428 và 708 đều có số dư là 151,704.

(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
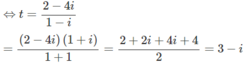

(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
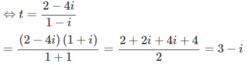
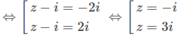
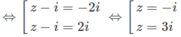
a) 20092010 :2010
Vì 2009 là số nguyên tốc và UCLN ( 2009,2011) = 1
nên 20092010 \(\equiv\) 1 ( mod 2011 )
b) 2009201020112012 : 2020
+ cắt 10 số thực hiện trước
2009201020 : 2020 ( dư 1960 )
+ tiếp tục tìm số dư của phép chia
1960112012 : 2020 ( dư 972 )
c) 1234567890987654321 : 2010
+ cắt 10 số thực hiện trước
1234567890 : 2010 ( dư 1770 )
+ tiếp tục tìm số dư của phép chia
1770987654321 : 2010 ( dư 471 )
Thi tốt !
Mình cảm ơn bạn nhiều nha
A ARMY kìa :)))
mình gửi thêm bạn giúp nhé