Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho abcd và dcba là các số chính phương có 4 chữ số khác nhau và dcba chia hết cho abcd .Tìm a,b,c,d


a,b,c,d là các chữ số
=> d<10
=> 0<a<3
mà 4 là số chẵn
=> dcba là số chẵn
=> a chẵn
=> a = 2
ta có 4. 2bcd = dcb2
=> d có thể nhận các giá trị 8 hoặc 9
mà một số có tận cùng là 8 nhân với 4 sẽ được số tận cùng là 2
=> d = 8
ta có 4. 2bc8 = 8cb2
<=> 4. (2000 + 100b + 10c + 8) = 8000 + 100c + 10b + 2
<=> 8000 + 400b + 40c + 32 = 8000 + 100c + 10b + 2
<=> 60c - 390b = 30
<=> 2c - 13b = 1
<=> 13b + 1 = 2c
mà 2c < 20
=> 13b < 19
=> b < 2
2c là số chẵn => b lẻ
=> b = 1
=> c = 7
thử lại thấy thỏa mãn
vậy số cần tìm là 2178

ọi số cần tìm là abcd
=> abcd.2 - 1004 = dcba
Dễ thấy a là số chẵn ( vì 2d - 4 là số chẵn) và a khác 0
mà d<10 suy ra a<6
=> a=2 hoặc a=4
với a=2 => d=3. thay vào ta tính được b = c = 0
a=4 => d=9
=> 4009.2 + bc.200 - 1004 = 9004 + cb.100
=> bc.20 - cb.10 = 199
=> bc.10=199 ( loại vì b,c là số tự nhiên)
Vậy số phải tìm là abcd = 2003


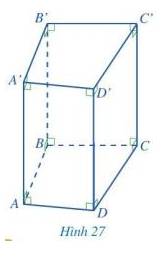
a) Đáy dưới ABCD và đáy trên A’B’C’D’ là hình tứ giác
b) Mặt bên AA’D’D là hình chữ nhật
c) Độ dài hai cạnh bên AA’ và DD’ bằng nhau.

\(\overline{abcd};\overline{dcba}\)là số tự nhiên có bốn chữ số
=> \(a,d\ne0\)
Và vì: \(4.\overline{abcd}=\overline{dcba}\)
=> a<3
TH1: a=1
Khi đó ta có: \(4.\overline{1bcd}=\overline{dcb1}\)
Loại vì không tồn tại số nhân với 4 được số tự nhiên tận cùng là 1
TH2: a=2
Khi đó ta có: \(4.\overline{2bcd}=\overline{dcb2}\)
=> d=3 hoặc d=8
+) Với d =3 ta có:
\(4.\overline{2bc3}=\overline{3cb2}\)loại ( vì 4.2=8>3)
+) Với d=8
ta có: \(4.\overline{2bc8}=\overline{8cb2}\)
<=> \(4.\left(2000+b.100+c.10+8\right)=8000+c.100+b.10+2\)
<=> \(390b-60c+30=0\)
<=> \(13b-2c+1=0\)
<=> \(c=\frac{13b+1}{2}\)
=> b=1 và c=7
Vậy số tự nhiên cần tìm là: 2178 và 4x2178=8712
Cô ơi e có cách giải mới mong cô xem qua
Số cần tìm có dạng \(\overline{abcd}\)
Ta có 4.\(\overline{abcd}=\overline{dcba}\Rightarrow\overline{dcba}⋮4\Rightarrow a\in\left\{0;1;4;6;8\right\}\)
Xét các trường hợp thấy \(a\in0\)và nếu \(a\ge4\)thì \(4.\overline{abcd}\ge4.4000>9999\ge\overline{dcba}\)
và a=2 =>\(\overline{abcd}=\overline{dcba}\ge4.2000=8000=>d\in\left\{8;9\right\}\)
Mà \(\overline{dcba}=4\overline{abcd}\Rightarrow4.d\)phải tận cùng bằng chữ số a.
Mặt khác :4.8=32;4.9=36=>d=8
Ta có \(\overline{dcba}=100.dc+ba=2.5.4.dc+ba⋮4\)
=>ba\(⋮\)4
Vì a\(⋮\)2 theo trên =>b\(\in\){1;3;5;7;9}
Xét các trường hợp của b
Nếu \(b\ge3\Rightarrow\overline{8cba}\ge4.2300=9200\)(vô lí )
Nếu b : 1=>\(\overline{8bc12}=4.\overline{2108}\)
=>8012+100c=4.2108+4.10.c
=>60c=420
=>c=420:60
=>c=7
Vậy \(\overline{abcd}=2178\)
Vì a,b,c,d là các chữ số
=> d<10
=> 0<a<3
mà 4 là số chẵn
=> dcba là số chẵn
=> a chẵn
=> a = 2
ta có 4. 2bcd = dcb2
=> d có thể nhận các giá trị 8 hoặc 9
mà một số có tận cùng là 8 nhân với 4 sẽ được số tận cùng là 2
=> d = 8
ta có 4. 2bc8 = 8cb2
<=> 4. (2000 + 100b + 10c + 8) = 8000 + 100c + 10b + 2
<=> 8000 + 400b + 40c + 32 = 8000 + 100c + 10b + 2
<=> 60c - 390b = 30
<=> 2c - 13b = 1
<=> 13b + 1 = 2c
mà 2c < 20
=> 13b < 19
=> b < 2
2c là số chẵn => b lẻ
=> b = 1
=> c = 7
thử lại thấy thỏa mãn
vậy số cần tìm là 2178