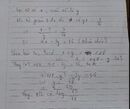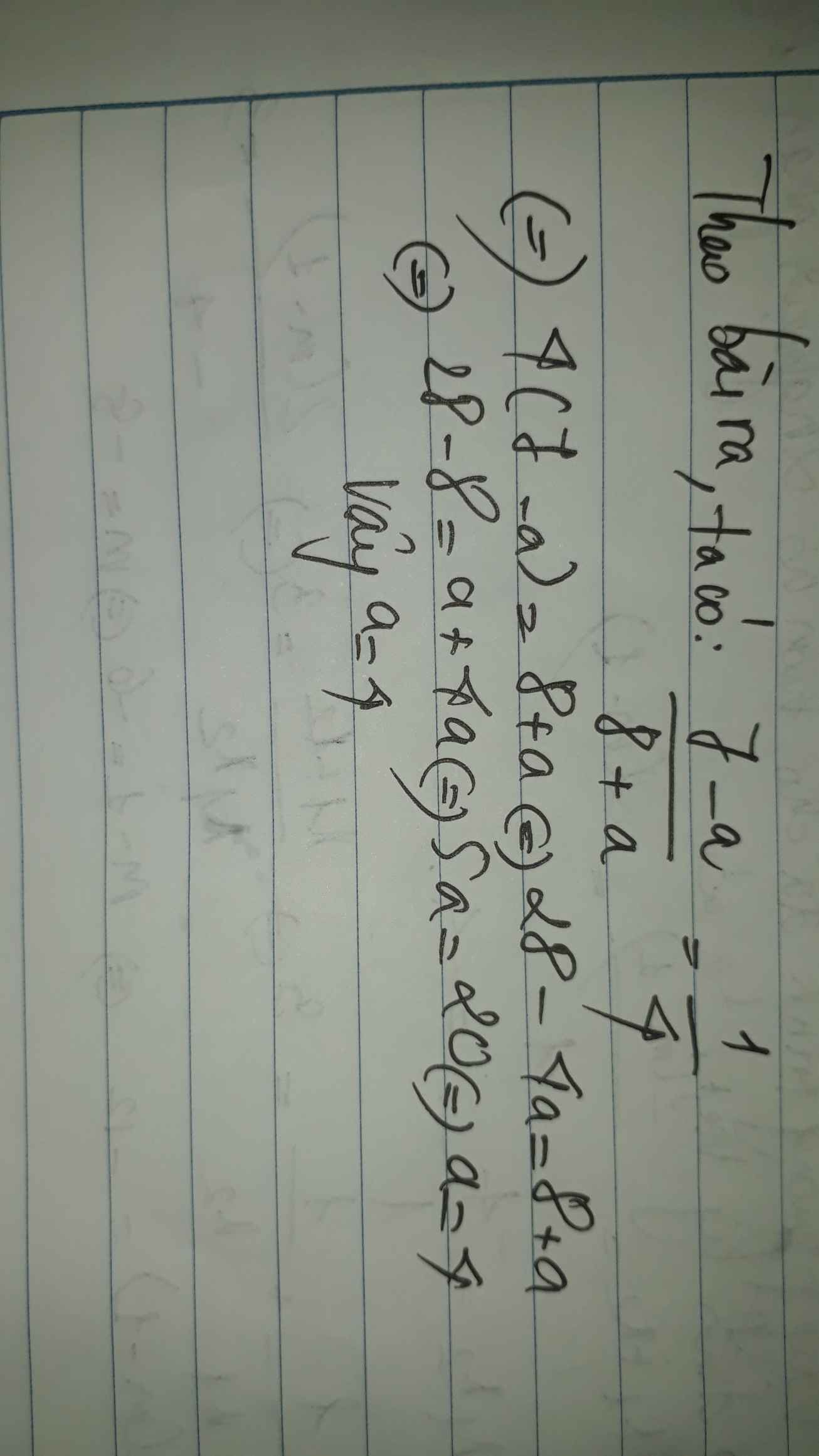Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. gọi số cần tìm là a
khi đó, ta có tử số mới là 54-a
mẫu số mới là 63+a
sau khi thêm ở mẫu số và bớt ở tử số ta được ps tối giản 4/5 tức là mẫu số mới gấp tử số mới 0,8 lần , ta có
63+a=0,8x(54-a)
63+a=0,8x54-0,8xa
63+a=43,2-0,8xa
63=43,2-0,9xa
0,9xa=63-43,2
0,9xa=19,8
a=19,8:0,9
a=22

Khi tử số bớt đi \(9\)đơn vị thì tổng của tử số mới và mẫu số là:
\(128-9=119\)
Nếu tử số mới là \(3\)phần thì mẫu số là \(4\)phần.
Tổng số phần bằng nhau là:
\(3+4=7\)(phần)
Tử số mới là:
\(119\div7\times3=51\)
Tử số là:
\(51+9=60\)
Mẫu số là:
\(128-60=68\)
Phân số cần tìm là: \(\frac{60}{68}\).

Ta có: \(\dfrac{7-a}{8+a}=\dfrac{1}{4}\)
\(\Leftrightarrow28-4a=a+8\)
\(\Leftrightarrow-5a=-20\)
hay a=4

Lời giải:
Giả sử số bớt đi là $a$. Ta có:
$\frac{17-a}{25-a}=\frac{1}{5}$
$5(17-a)=25-a$
$85-5a=25-a$
$85-25=5a-a$
$60=4a$
$a=60:4$
$a=15$
Gọi só tự nhiên cần tìm là x
Theo đề, ta có phương trình:
\(\dfrac{17-x}{25-x}=\dfrac{1}{5}\)
\(\Leftrightarrow85-5x=25-x\)
\(\Leftrightarrow-4x=-60\)
hay x=15

Phân số P có tử số = 45; mẫu số = 1/2(21+29)*9 = 225. Nên phân số P = 1/5
Để bớt P: tử 1 số mẫu 1 số để được 1 phân số mới = P thì cặp số ấy cũng tỷ lệ với nhau theo tỷ số 1/5.
Nên cặp số đó là 5 và 25.

gọi TS là x
Ms là x + 8
Khi thêm ở TS 3 đv và bớt ở MS 3 đv thì ta có p/s mới là :
x + 3/x + 8 - 3 = 5/6
<=>( x +3 ). 6 = ( x + 5 ) . 5
<=> 6x + 18 = 5x + 25
<=> x = 25 - 18
<=> x = 7
Vậy ts là 7 và ms là 15
sau khi thêm ở tử 3 đơn vị và bớt 3 đơn vị ở mẫu thì hiệu giữa ts và ms mới là:
8-3-3=2(đơn vị)
vậy mẫu số mới hơn ts mới số phần bằng nhau là:
6-5=1(phần)
mẫu số mới là:
2:1x6=12
mẫu số ban đầu là:
12+3=15
tử số ban đầu là:
15-8=7
Vậy ps đó là \(\frac{7}{15}\)

Gọi số cần cộng thêm vào cả tử và mẫu là a
Theo bài ra ta có:
\(\frac{-4+a}{7+a}=\frac{1}{2}\)
=> 2(a - 4) = 7 + a
=> 2a - 4 = 7 + a
=> 2a - a = 7 + 4
=> a = 11
2/ \(\frac{-5}{-9}=\frac{5}{9}\)
Gọi số cần thêm vào mẫu và bớt đi ở tử là b
Theo bài ra ta có:
\(\frac{5-b}{9+b}=\frac{-7}{12}\)
=> 12(5 - b) = -7(9 + b)
=> 60 - 12b = -63 - 7b
=> 60 + 63 = -7b + 12b
=> 123 = 5b
=> b = \(\frac{123}{5}\)