Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(\hept{\begin{cases}\left(\frac{1}{x}+y\right)+\left(\frac{1}{x}-y\right)=\frac{5}{8}\\\left(\frac{1}{x}+y\right)-\left(\frac{1}{x}-y\right)=-\frac{3}{8}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{2}{x}=\frac{5}{8}\\2y=-\frac{3}{8}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{16}{5}\\y=-\frac{3}{16}\end{cases}}}\)
\(Pt\Leftrightarrow3x^2+12x+4y^2+3y+5=0\)
Coi pt trên là pt bậc 2 ẩn x
Ta có : \(\Delta'=36-12y^2-9y-15\)
\(=-12y^2-9y+21\)
Pt có nghiệm \(\Leftrightarrow\Delta'=-12y^2-9y+21\ge0\)
\(\Leftrightarrow-\frac{7}{4}\le y\le1\)
Mà \(y\inℤ\Rightarrow y\in\left\{-1;0;1\right\}\)
Rồi làm nốt
a) (I):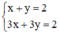 
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x +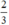 
có a’ = -1 ; b’ =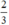 
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
b) (II):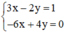 
Xét: (d): 3x – 2y = 1 hay (d):
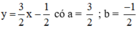
(d’): -6x + 4y = 0 hay (d’):
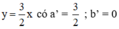
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Kiến thức áp dụng
+ Xét hệ (I):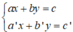 
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Với câu a)bạn nhân cả 2 vế cho 12 rồi ép vào dạng bình phương 3 số
Câu b)bạn nhân cho 8 mỗi vế rồi ép vào bình phương 3 số
\(\Leftrightarrow3\left(x+1\right)^2+4y^2+3y-7=0\)
\(\Leftrightarrow4y^2+3y-7=-3\left(x+1\right)^2\le0\)
\(\Rightarrow4y^2+3y-7\le0\Rightarrow-\frac{7}{4}\le y\le1\)
\(\Rightarrow y=\left\{-1;0;1\right\}\)
Thay lần lượt y vào pt ban đầu thấy chỉ có \(y=1\) thỏa mãn, khi đó \(x=-1\)
ĐKXĐ: \(x\ge-\frac{1}{2}\)
\(\sqrt{2x+1}+x^2-3x+1=0\)
\(\Rightarrow\sqrt{2x+1}=-x^2+3x-1\)
\(\Rightarrow2x+1=x^4-6x^3+11x^2-6x+1\)
\(\Rightarrow x^4-6x^3+11x^2-8x=0\)
\(\Rightarrow x\left(x^3-6x^2+11x-8\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x^3-6x^2+11x-8=0\left(1\right)\end{cases}}\)
(1) => bấm máy ta nhận đc 1 nghiệm như mà lẻ quá
Vậy có 2 nghiệm
\(\sqrt{2x+1}=t\ge0\)\(\Rightarrow x=\frac{t^2-1}{2}\)
thay vài phương trình đã cho và phân tích nhân tử, ta được:
\(pt\rightarrow\left(t+1\right)\left(t^3-t^2-7t+11\right)=0\)
\(\Leftrightarrow t^3-t^2-7t+11=0\text{ (1)}\)\(do\text{ }t+1>0\)
Bấm máy tính thấy phương trình này chỉ có 1 nghiệm âm, do đó ta chứng minh phương trình này ko có nghiệm dương
\(\left(1\right)\Leftrightarrow t\left(t^2-4t+4\right)+3t^2-11t+11=0\)
\(\Leftrightarrow t\left(t-2\right)^2+3\left(t-\frac{11}{6}\right)^2+\frac{11}{12}=0\)
Thấy ngay phương trình này có VT > 0 nên vô nghiệm.
Vậy phương trình đã cho VÔ NGHIỆM.
\(\left\{{}\begin{matrix}x^2+2xy-3y^2=-4\left(1\right)\\2x^2+xy+4y^2=5\left(2\right)\end{matrix}\right.\)\(với\)\(y=0\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}x^2=-4\\2x^2=5\end{matrix}\right.\)\(\left(loại\right)\)
\(y\ne0\) \(đặt:x=t.y\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}t^2y^2+2ty^2-3y^2=-4\left(3\right)\\2t^2y^2+ty^2+4y^2=5\left(4\right)\end{matrix}\right.\)
\(\Leftrightarrow5t^2y^2+10ty^2-15y^2=-8t^2y^2-4ty^2-16y^2\)
\(\Leftrightarrow13t^2y^2+14ty^2+y^2=0\)
\(\Leftrightarrow13t^2+14t+1=0\Leftrightarrow\left[{}\begin{matrix}t=-\dfrac{1}{13}\\t=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{13}y\left(5\right)\\x=-y\left(6\right)\end{matrix}\right.\)
\(thay\left(5\right)và\left(6\right)\) \(lên\left(1\right)hoặc\left(2\right)\Rightarrow\left(x;y\right)=\left\{\left(1;-1\right);\left(-1;1\right);\left(-\dfrac{1}{\sqrt{133}};\dfrac{13}{\sqrt{133}}\right)\right\}\)
\(pt:x^4-4x^3+x^2+6x+m+2=0\)
\(\Leftrightarrow x^4-4x^3+4x^2-3x^2+6x+m+2=0\)
\(\Leftrightarrow\left(x^2-2x\right)^2-3\left(x^2-2x\right)+m+2=0\left(1\right)\)
\(đặt:x^2-2x=t\ge-1\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-3t=-m-2\)
\(xét:f\left(t\right)=t^2-3t\) \(trên[-1;+\text{∞})\) \(và:y=-m-2\)
\(\Rightarrow f\left(-1\right)=4\)
\(f\left(-\dfrac{b}{2a}\right)=-\dfrac{9}{4}\)
\(\left(1\right)\) \(có\) \(3\) \(ngo\) \(pb\Leftrightarrow-m-2=4\Leftrightarrow m=-6\)
ĐK \(x\ne0\)
Chia cả 2 vế cho \(\frac{1}{x}\)ta được
\(\frac{3}{3x-4+\frac{1}{x}}+\frac{13}{3x+2+\frac{1}{x}}=6\)
Đặt \(3x+\frac{1}{x}=y\)
\(\Rightarrow\frac{3}{y-4}+\frac{13}{y+2}=6\)
\(\Leftrightarrow16y-46=6\left(y-4\right)\left(y+2\right)\)
Đến đây tự giải nhé (Phá ngoặc rồi ghép cặp lại)
x,y là số nguyên tố đúng ko? bn có nhiueeuf câu hỏi nên mik trả lời nhầm.(ko phait thì thui nhé)
\(\left(3x^2+6x+3\right)+\left(3y^2+3y+1\right)+y^2-8=0\)
\(\Leftrightarrow3\left(x+1\right)^2+3\left(y+\frac{1}{2}\right)^2-\frac{9}{4}-8=0\)
\(\Leftrightarrow12\left(x+1\right)^2+3\left(y+1\right)^2=41\)
\(\Rightarrow12\left(x+1\right)^2\le41\Rightarrow\left(x+1\right)^2\le3\Rightarrow x+1\in\left\{1;0;-1\right\}\Rightarrow x\in\left\{0;-1;-2\right\}\)
Bạn làm nốt