
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

29 tháng 4 2019
Vì \(3x,159\) đều chia hết cho 3 nên 17y chia hết cho 3.
Mà 17 là số nguyên tố nên y chia hết cho 3.
Đặt \(y=3t\left(t\in Z\right)\)
Thay vào phương trình,ta có:
\(3x+17\cdot3t=159\)
\(\Rightarrow x+17t=53\)
\(\Rightarrow x=53-17t\)
Do đó:\(\hept{\begin{cases}y=3t\\x=53-17t\end{cases}}\)
Vậy phương trình có vô số nghiệm nguyên được xác định bởi công thức:\(\hept{\begin{cases}y=3t\\x=53-17t\end{cases}}\) với t là số nguyên tùy ý.
TP
0

LC
0


CM
17 tháng 8 2019
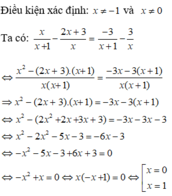
Kết hợp điều kiện thì nghiệm của phương trình đã cho là x = 1
Chọn đáp án D

CM
29 tháng 3 2017
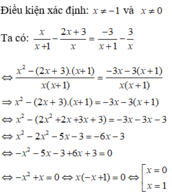
Kết hợp điều kiện thì nghiệm của phương trình đã cho là x = 1
Chọn đáp án D

Nghiệm phương trình là x thuộc R và y=159-3x/17
Vì 3x,1593x,159 đều chia hết cho 3 nên 17y chia hết cho 3.
Mà 17 là số nguyên tố nên y chia hết cho 3.
Đặt y=3t(t∈Z)y=3t(t∈Z)
Thay vào phương trình,ta có:
3x+17⋅3t=1593x+17⋅3t=159
⇒x+17t=53⇒x+17t=53
⇒x=53−17t⇒x=53−17t
Do đó:\hept{y=3tx=53−17t\hept{y=3tx=53−17t
Vậy phương trình có vô số nghiệm nguyên được xác định bởi công thức:\hept{y=3tx=53−17t\hept{y=3tx=53−17t với t là số nguyên tùy ý.