K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 6 2019
-10x3 + 7x + 13 = 0
<=> 10x3-7x-13=0
<=>\(10\left(x^3-\frac{7}{10}x-\frac{13}{10}\right)=0\)
\(\Leftrightarrow x^3-\frac{7}{10}x-\frac{13}{10}=0\)
HN
29 tháng 6 2019
ღ๖ۣۜLinh's ๖ۣۜLinh'sღ] ★we are one★ Bạn ơi sao lại biến đổi từ cộng thành trừ được?
PN
1
NN
13 tháng 4 2019
\(x^2-7x+2-2\left(x+1\right)=0\)
\(\Leftrightarrow x^2-7x+2-2x-2=0\)
\(\Leftrightarrow x^2-9x=0\Leftrightarrow x\left(x-9\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=9\end{cases}}\)
Vậy đa thức có 2 nghiệm là x = 0, x = 9
H9
HT.Phong (9A5)
CTVHS
2 tháng 8 2023
a) \(A=-11x^5+4x-12x^2+11x^5+13x^2-7x+2\)
\(A=\left(-11x^5+11x^5\right)+\left(-12x^2+13x^2\right)+\left(4x-7x\right)+2\)
\(A=0+x^2+\left(-3x\right)+2\)
\(A=x^2-3x+2\)
Bậc của đa thức là: \(2\)
Hệ số cao nhất là: \(1\)
b) Ta có: \(M\left(x\right)=A\left(x\right)\cdot B\left(x\right)\)
\(\Rightarrow M\left(x\right)=\left(x^2-3x+2\right)\cdot\left(x-1\right)\)
\(\Rightarrow M\left(x\right)=x^3-x^2-3x^2+3x+2x-2\)
\(\Rightarrow M\left(x\right)=x^3-4x^2+5x-2\)
c) A(x) có nghiệm khi:
\(A\left(x\right)=0\)
\(\Rightarrow x^2-3x+2=0\)
\(\Rightarrow x^2-x-2x+2=0\)
\(\Rightarrow x\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
LL
1
LH
31 tháng 3 2017
a) \(f\left(x\right)=x^2+7x-8=0\)
\(\Leftrightarrow f\left(x\right)=x^2-x+8x-8=0\)
\(\Leftrightarrow f\left(x\right)=\left(x^2-x\right)+\left(8x-8\right)=0\)
\(\Leftrightarrow f\left(x\right)=x\left(x-1\right)+8\left(x-1\right)=0\)
\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x+8\right)=0\)
\(\Rightarrow x-1=0\) hoặc \(x+8=0\)
Nếu \(x-1=0\Rightarrow x=1\)
Nếu \(x+8=0\Rightarrow x=-8\)
Vậy đa thức f(x) có nghiệm là 1 và -8
b) \(k\left(x\right)=5x^2+9x+4=0\)
\(\Leftrightarrow k\left(x\right)=5x^2+5x+4x+4=0\)
\(\Leftrightarrow k\left(x\right)=\left(5x^2+5x\right)+\left(4x+4\right)=0\)
\(\Leftrightarrow k\left(x\right)=5x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow k\left(x\right)=\left(x+1\right)\left(5x+4\right)=0\)
\(\Rightarrow x+1=0\) hoặc \(5x+4=0\)
Nếu \(x+1=0\Rightarrow x=-1\)
Nếu \(5x+4=0\Rightarrow x=-\frac{4}{5}\)
Vậy đa thức k(x) có nghiệm là -1 và -4/5
CM
30 tháng 1 2018
c. x = 3, x = -3 có là nghiệm của N(x) vì N(3) = N(-3) = 0 (0.5 điểm)
18 tháng 4 2023
Đặt `6x^2+7x=0`
`-> 6x*x+7x=0`
`-> x(6x+7)=0`
`->`\(\left[{}\begin{matrix}x=0\\6x+7=0\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\6x=0-7\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\6x=-7\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\x=-\dfrac{7}{6}\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x=0, x=-7/6`.
`@`\(\text{dn inactive.}\)
12 tháng 5 2022
Ta có \(x^2-7x+8=0\Leftrightarrow x^2-\dfrac{2.7}{2}x+8=0\)
\(\Leftrightarrow x^2-7x+\dfrac{49}{4}-\dfrac{49}{4}+8=0\Leftrightarrow\left(x-\dfrac{7}{2}\right)^2-\dfrac{17}{4}=0\)
\(\left[{}\begin{matrix}x-\dfrac{7}{2}=\dfrac{\sqrt{17}}{2}\\x-\dfrac{7}{2}=-\dfrac{\sqrt{17}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{17}+7}{2}\\x=\dfrac{-\sqrt{17}+7}{2}\end{matrix}\right.\)
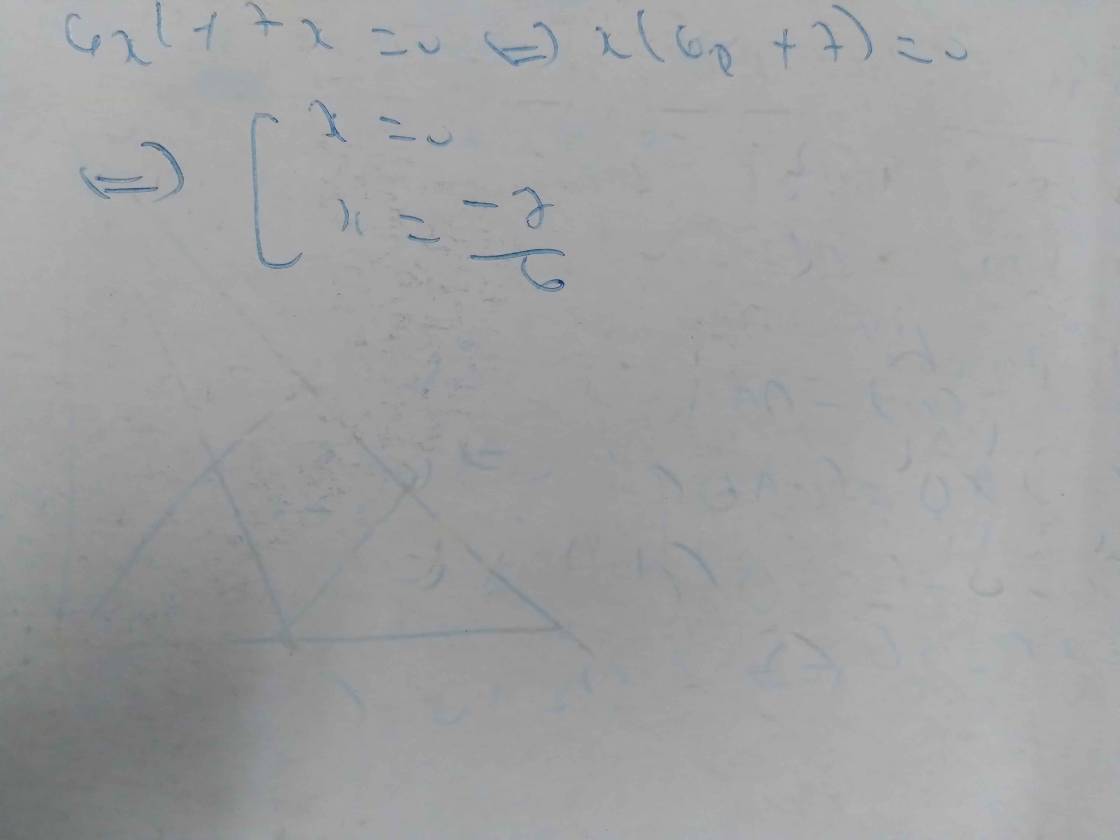
-10x3 + 7x + 13 = 0
\(\Leftrightarrow x=\frac{\left(39\sqrt{15}+148,758193051677\right)^{\frac{1}{3}}}{\sqrt[3]{4}\sqrt{15}}+\frac{7\sqrt[3]{4}}{2\sqrt{15}\left(39\sqrt{15+148,758193051677}\right)^{\frac{1}{3}}}\)
\(\Leftrightarrow x=-\frac{\left(\sqrt{22129}+13\sqrt{27}\sqrt{5}\right)^{\frac{2}{3}}\left(\sqrt{3}i+1\right)-7\sqrt[3]{2}\sqrt{3}i+7\sqrt[3]{2}}{\sqrt[3]{32}\sqrt{3}\sqrt{5}\left(\sqrt{22129}+13\sqrt{27}\sqrt{5}\right)^{\frac{1}{3}}}\)
\(\Leftrightarrow x=\frac{\left(\sqrt{22129}+13\sqrt{27}\sqrt{5}\right)^{\frac{2}{3}}\left(\sqrt{3}i-1\right)-7\sqrt[3]{2}\sqrt{3}i-7\sqrt[3]{2}}{\sqrt[3]{32}\sqrt{3}\sqrt{5}\left(\sqrt{22129}+13\sqrt{27}\sqrt{5}\right)^{\frac{1}{3}}}\)
Ơ, đề bài là tìm nghiệm mà bạn. Bạn làm cái gì đấy?