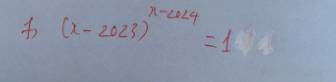Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(A=1+3+3^2+3^3+...+3^{2017}\)
\(3A=3\left(1+3+3^2+3^3+...+3^{2017}\right)\)
\(=3+3^2+3^3+3^4+...+3^{2018}\)\(3A-A=\left(3+3^2+3^3+3^4+...+3^{2018}\right)-\left(1+3+3^2+3^3+...+3^{2017}\right)\)\(2A=3^{2018}-1\Rightarrow A=\frac{3^{2018}-1}{2}\)
Vậy \(A=\frac{3^{2018}-1}{2}\)
gọi bieu thuc tren la A
A= 1+3+3^2+..+3^2017
3A= 3.(1+3+362+..+3^2017)
3A=3+3^2+3^3+...+3^2018
3A - A= (3+ 3^2+3^3+...+3^2018) - (1+3+3^2+...+3^2017)
2A= 3^2018 - 1
=> A= \(\frac{3^{2018}-1}{2}\)

ta thấy:2017 không chia hết cho 5 Từ đó áp dụng tính chất nếu một số hạng trong một tổng không chia hết cho số đó =>Tổng đó không chia hết cho số đó =>Akhông chia hết cho 5
Mọi người giúp mik thì ghi đầy đủ giùm mik
mik mong rằng mikf đc k cho người nhanh nhất, chính xác nhất
thanks you


1. Tìm x
a) 1+2+3+...+x = 210
=> \(\frac{x\left(x+1\right)}{2}=210\)
=> x = 20
b) \(32.3^x=9.3^{10}+5.27^3\)
=>\(32.3^x=9.3^{10}+5.3^9\)(\(27^3=\left(3^3\right)^3=3^9\))
=>\(32.3^x=9.3.3^9+5.3^9\)
=>\(32.3^x=3^9\left(9.3+5\right)\)
=>\(32.3^x=3^9.32\)
=>x = 9
2.
Ta có 2A = 3A - A
=> 2A = \(3\left(1+3+3^2+3^3+....+3^{10}\right)\)\(-\)\(1-3-3^2-3^3-....-3^{10}\)
=> 2A = \(3+3^2+3^3+.....+3^{11}-\)\(1-3-3^2-3^3-...-3^{10}\)
=> 2A = \(3^{11}-1\)
=> 2A+1 = \(3^{11}-1+1\)=\(3^{11}\)
=> n = 11
Ta có : a)1 + 2 + 3 + ... + x = 210
=> \(\frac{x\left(x+1\right)}{2}=210\)
=> x(x + 1) = 420
=> x(x + 1) = 20.21
=> x = 20

Có :
242 chia hết cho 2
312 chia hết cho 2
Để A chia hết cho 2
=> n chia hết cho 2
Đặt n=2k
Vậy A chia hết cho 2 <=> n = 2k ( hay chia hết cho 2 )

(\(x\) - 2023)\(x-2024\) = 1
⇒ \(\left[{}\begin{matrix}x\ne2023;x-2024=0\\x-2023=1\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=2024\\x=2024\end{matrix}\right.\)
Vậy \(x=2024\)
(x - 2023)ˣ⁻²⁰²⁴ = 1
(x - 2023)ˣ⁻²⁰²⁴ = (x - 2023)⁰ (x ≠ 2023)
x - 2024 = 0
x = 2024 (nhận)
Vậy x = 2024