K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AT
0
PJ
0
TN
3
29 tháng 7 2018
32^n / 16^n = 2048
(32/16)^n = 2048
2^n = 2048
2^n = 2^11
n = 11
Vậy n = 11.
29 tháng 7 2018
\(\frac{32^n}{16^n}=2048\)
\(\Rightarrow\left(\frac{32}{16}\right)^n=2048\)
\(\Rightarrow2^n=2048\)
\(\Rightarrow2^n=2^{11}\)
\(\Rightarrow n=11\)
Vậy n = 11
_Chúc bạn học tốt_
MH
2
TN
17 tháng 7 2017
Theo đề ta có : \(32^{-n}.16^n=2048\)
\(\Rightarrow\frac{1}{32^n}.16^n=2048\)
\(\Rightarrow\frac{16^n}{32^n}=2048\)
\(\Rightarrow\left(\frac{16}{32}\right)^n=\left(\frac{1}{2}\right)^n=2048\)
\(\Rightarrow\frac{1}{2^n}=2048\)
\(\Rightarrow2^n=\frac{1}{2048}\)
\(\Rightarrow2^n=\frac{1}{2^{11}}\Rightarrow1=2^n.2^{11}\)
\(\Rightarrow2^n=2^{-11}\Rightarrow n=-11\) ( bởi vì tích của 2 số nghịch đảo bao giờ cũng bằng 1)
LD
17 tháng 7 2017
qui ước \(x^{-a}=\frac{1}{x^a}\)
ta có
\(32^{-n}.16^n=2048\Rightarrow\frac{1}{32^n}.16^n=2^{10}\Rightarrow\frac{16^n}{32^n}=2^{10}\)
\(\Rightarrow\left(\frac{16}{32}\right)^n=\frac{1}{2^n}=2^{10}\Rightarrow2^{-n}=2^{10}\Rightarrow-n=10\Rightarrow n=-10\)
2T
24 tháng 8 2019
a) \(\frac{1}{9}.27^n=3^n\)
\(\Leftrightarrow3^{-2}.3^{3n}=3^n\)
\(\Leftrightarrow3^{3n-2}=3^n\)
\(\Leftrightarrow3n-2=n\)
\(\Leftrightarrow2n=2\)
\(\Leftrightarrow n=1\)
2T
24 tháng 8 2019
b)\(3^{-2}.3^4.3^n=3^7\)
\(\Leftrightarrow3^{2+n}=3^7\)
\(\Leftrightarrow2+n=7\)
\(\Leftrightarrow n=5\)
BN
2
11 tháng 11 2016
a)\(32^{-n}\cdot16^n=2048\)
\(\left(2^5\right)^{-n}\cdot\left(2^4\right)^n\)=2048
\(2^{-5n}\cdot2^{4n}\)=\(2^{11}\)
\(2^{-5n+4n}=2^{11}\)
\(2^{-x}=2^{11}\)
\(\Rightarrow x=-11\)
b)\(2^{-1}\cdot2^n+4\cdot2^n=9\cdot2^5\)
\(\frac{1}{2}\cdot2^n+4\cdot2^n=288\)
\(2^n\left(\frac{1}{2}+4\right)=288\)
\(2^n\cdot\frac{9}{2}=288\)
\(2^n=288:\frac{9}{2}\)
\(2^n=64\)
\(2^n=2^6\)
\(\Rightarrow n=6\)
11 tháng 11 2016
a) 32-n . 16n = 2048
\(\frac{1}{32n}\) . 16n = 2048
\(\frac{1}{2^n.16^n}\) . 16n = 2048
\(\frac{1}{2^n}\) = 2048
2-n = 2048
2-n = 211
\(\Rightarrow\) -n = 11
\(\Rightarrow\) n = -11
Vậy n = -11
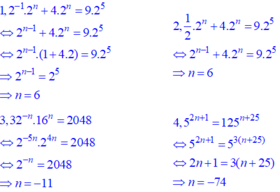
32^-n.16^n=2048=>1/32^n.16^n=2048
=>1/(16^n.2^n).16^N=2048
=>1/2^n=2048=>n= -11