Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |

\(f\left(x\right)=4x+\frac{3}{\left(x+1\right)^2}=2x+2+2x+2+\frac{3}{\left(x+1\right)^2}-4\ge3\sqrt[3]{\left(2x+2\right)^2.\frac{3}{\left(x+1\right)^2}}-4\)
\(=3\sqrt[3]{48}-4\)
Dấu \(=\)khi \(2x+2=\frac{3}{\left(x+1\right)^2}\Leftrightarrow\left(x+1\right)^3=\frac{3}{2}\Leftrightarrow x=\sqrt[3]{\frac{3}{2}}-1\).

\(\sqrt{x^2-4x+5}=\sqrt{x^2-4x+4+1}=\sqrt{\left(x-2\right)^2+1}>=1\forall x\)
=>\(y=\dfrac{1}{\sqrt{x^2-4x+5}}< =\dfrac{1}{1}=1\forall x\)
Vậy: TGT là \(T=(-\infty;1]\)

Lời giải:
Áp dụng BĐT Mincopxky:
\(y=\sqrt{x^2+4x+8}+\sqrt{x^2-4x+8}=\sqrt{(x+2)^2+4}+\sqrt{(x-2)^2+4}\)
\(=\sqrt{(x+2)^2+2^2}+\sqrt{(2-x)^2+2^2}\geq \sqrt{(x+2+2-x)^2+(2+2)^2}\)
\(=\sqrt{32}=4\sqrt{2}\)
Vậy $y_{\min}=4\sqrt{2}$ khi $x=0$

1. 1/x + 2/1-x = (1/x - 1) + (2/1-x - 2) + 3
= 1-x/x + (2-2(1-x))/1-x + 3
= 1-x/x + 2x/1-x + 3 >= 2√2 + 3
Dấu "=" xảy ra khi x =√2 - 1
2. a = √z-1, b = √x-2, c = √y-3 (a,b,c >=0)
=> P = √z-1 / z + √x-2 / x + √y-3 / y
= a/a^2+1 + b/b^2+2 + c/c^2+3
a^2+1 >= 2a => a/a^2+1 <= 1/2
b^2+2 >= 2√2 b => b/b^2+2 <= 1/2√2
c^2+3 >= 2√3 c => c/c^2+3 <= 1/2√3
=> P <= 1/2 + 1/2√2 + 1/2√3
Dấu = xảy ra khi a^2 = 1, b^2 = 2, c^2 =3
<=> z-1 = 1, x-2 = 2, y-3 = 3
<=> x=4, y=6, z=2

\(P=\dfrac{4x^2+2xy-\left(x^2+y^2\right)}{2xy-2y^2+3\left(x^2+y^2\right)}=\dfrac{3x^2+2xy-y^2}{3x^2+2xy+y^2}\)
Biểu thức này không tồn tại max mà chỉ tồn tại min
\(P=\dfrac{-2\left(3x^2+2xy+y^2\right)+9x^2+6xy+y^2}{3x^2+2xy+y^2}=-2+\dfrac{\left(3x+y\right)^2}{2x^2+\left(x+y\right)^2}\ge-2\)


\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
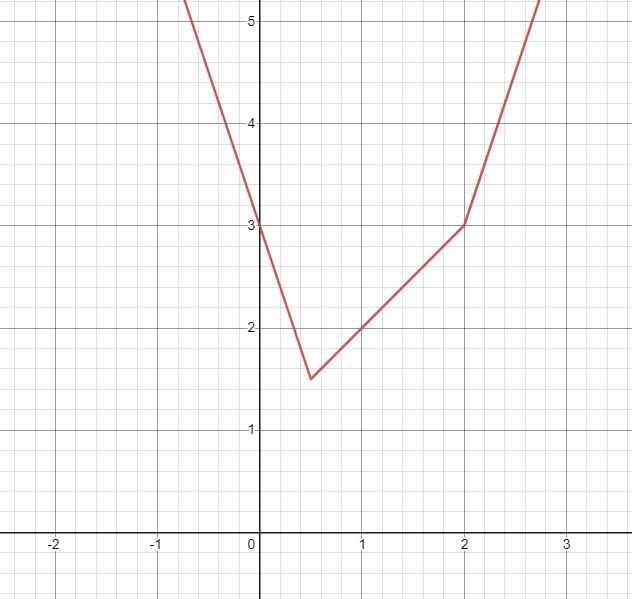
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)
Đặt \(\sqrt{x^2+4x+5}=t\Rightarrow t\in\left[\sqrt{5};\sqrt{17}\right]\)
\(\Rightarrow y=f\left(t\right)=t^2-2t+7\)
\(-\dfrac{b}{2a}=1\notin\left[\sqrt{5};\sqrt{17}\right]\)
\(f\left(\sqrt{5}\right)=10+4\sqrt{5}\) ; \(f\left(\sqrt{17}\right)=22+4\sqrt{17}\)
\(\Rightarrow y_{min}=10+4\sqrt{5}\) ; \(y_{max}=22+4\sqrt{17}\)
|x^2-x-m|=2x-1.Tìm m để pt có 4 nghiệm phân biệt
giúp ạ