Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
y ' = x 2 - 2 x + ( m - 1 ) .
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
⇒ Δ = ( - 1 ) 2 - ( m - 1 ) = - m + 2 ≤ 0 ⇔ m > 2

a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng ( - ∞ ; m), (m; + ∞ ) khi và chỉ khi:
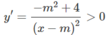
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3

\(y'=-x^2+2\left(a-1\right)x+a+3\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x\in\left(0;3\right)\) ta có:
\(-x^2+2\left(a-1\right)x+a+3\ge0\)
\(\Leftrightarrow\left(2x+1\right)a\ge x^2+2x-3\)
\(\Rightarrow a\ge\dfrac{x^2+2x-3}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) với \(x\in\left(0;3\right)\)
\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\Rightarrow a\ge\dfrac{12}{7}\)

Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀ x ⇔ ∆ ' = 4m2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.

Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4 m 2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.
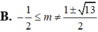
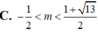
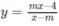 đồng biến trên từng khoảng xác định;
đồng biến trên từng khoảng xác định;

câu này bấm máy cho nhanh bạn ơi, giải kia k chắc lỡ sai uổn lắm..