NA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
5 tháng 1 2021
1.
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta=25-12m>0\\x_1^2+x_2^2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(x_1+x_2\right)^2-2x_1x_2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(2m-3\right)^2-2\left(m^2-4\right)< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\2m^2-12m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \dfrac{25}{12}\)
KC
0
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2021
Với \(x=0\) ko phải nghiệm
Với \(x\ne0\) chia 2 vế cho \(x^2\) ta được:
\(x^2+\dfrac{1}{x^2}+3x+\dfrac{3}{x}+m=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)+m-2=0\) (1)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow x^2-tx+1=0\) (2)
(2) có 2 nghiệm pb khi và chỉ khi:
\(\Delta=t^2-4>0\Rightarrow\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
Khi đó (1) trở thành:
\(t^2+3t+m-2=0\) (3)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (3) có 2 nghiệm pb thỏa mãn \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
(3) \(\Leftrightarrow t^2+3t-2=-m\)
Đặt \(f\left(t\right)=t^2+3t-2\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=8\)
Đồ thị hàm \(f\left(t\right)\):
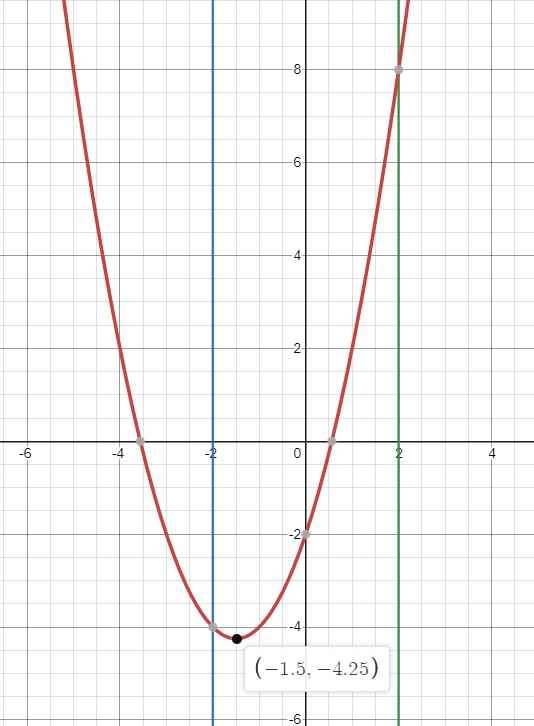
Từ đồ thị ta thấy \(y=-m\) cắt \(y=f\left(t\right)\) tại 2 điểm đều nằm ngoài \(\left[-2;2\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}-\dfrac{17}{4}< -m< -4\\-m>8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4< m< \dfrac{17}{4}\\m< -8\end{matrix}\right.\)
26 tháng 7 2021
thầy cho em hỏi làm mấy dạng tìm điều kiện này thạo thì nên học qua tư liệu nào ? Thầy có thể cho e một số file chuyên đề về mấy dạng này đc không?
NN
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 11 2019
a/ Chắc là bạn ghi nhầm đề? Số cuối là số 9 mới đúng, chứ 27 thì câu này vô nghiệm
\(x^4+4x^3+4x^2+8x^2+12x+27=0\)
\(\Leftrightarrow x^2\left(x+2\right)^2+8\left(x+\frac{3}{4}\right)^2+\frac{45}{2}=0\)
Vế phải dương nên pt vô nghiệm
b/ Nhận thấy \(x=0\) không phải nghiệm, chia 2 vế cho \(x^2\) ta được:
\(x^2+\frac{1}{x^2}-5\left(x-\frac{1}{x}\right)+6=0\)
Đặt \(x-\frac{1}{x}=a\Rightarrow x^2+\frac{1}{x^2}=a^2+2\)
\(\Rightarrow a^2+2-5a+6=0\)
\(\Leftrightarrow a^2-5a+8=0\Rightarrow\) pt vô nghiệm
Lại nhầm đề nữa???? Dấu thứ 2 là dấu + thì pt này có nghiệm đẹp
25 tháng 2 2022
Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2
DY
1
16 tháng 11 2021
\(hình\) \(như\) \(sai\) \(bn\) \(ạ\) \(vì:m=-2\Rightarrow\left\{{}\begin{matrix}\left(1\right):x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x1=1\\x2=-2\end{matrix}\right.\\\left(2\right)x^2-2x+1=0\Rightarrow\left[{}\begin{matrix}x1=1\\x2=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow S1\ne S2\Rightarrow\left(1\right)\ne\left(2\right)\)
\(x^2+x+m=0\left(1\right)\)
\(x^2+mx+1=0\left(2\right)\)
\(tương\) \(đương\) \(TH1:\left(1\right)\left(2\right)vô-nghiệm\Leftrightarrow\left\{{}\begin{matrix}\Delta1< 0\\\Delta2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-4m< 0\\m^2-4< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{1}{4}\\-2< m< 2\end{matrix}\right.\)\(\Leftrightarrow\dfrac{1}{4}< m< 2\)
\(TH2:\left(1\right)\left(2\right)có-ngo-kép-chung\)
\(\left(2\right)\Rightarrow\Delta=0\Rightarrow m^2-4=0\Leftrightarrow m=\pm2\Rightarrow\left(1\right):x^2+x-2=0\Leftrightarrow\left[{}\begin{matrix}x1=1\\x2=-2\end{matrix}\right.\left(ktm\right)\)
\(với:m=2\Rightarrow\left(1\right):x^2+x+2=0\left(vô-ngo\right)\)
\(\Rightarrow\dfrac{1}{4}< m< 2\) \(thì....\)
16 tháng 11 2021
\(\left(1\right)\Leftrightarrow m=-x^2-x\)
Thay vào (2)
\(\left(2\right)\Leftrightarrow x^2-\left(x^2+x\right)x+1=0\\ \Leftrightarrow1-x^3=0\\ \Leftrightarrow\left(1-x\right)\left(x^2+x+1\right)=0\\ \Leftrightarrow x=1\left(x^2+x+1>0\right)\\ \Leftrightarrow m=-1-1=-2\)
Thôi bt làm rồi nha :)